Leasing a Car

Once upon a time I found a magic formula for the monthly payments, when leasing a car.
See Lease Payments.

I decided to try to make sense of it, so generated an Excel spreadsheet which looks like so:

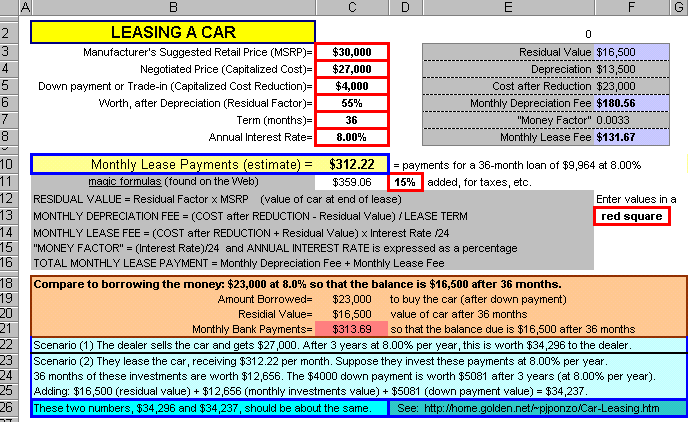
You stick new values into the red squares.

If you think it might be helpful, you can download the spreadsheet (as a .ZIP'd file):

To download the file, RIGHT-click here and Save Target.

I forgot. You also get a chart, like so
where the various values can, of course, be changed at will.

Okay, let's generate a formula for the monthly lease payments.

The car dealer can either:

  1. Sell the car for $A, invest it at I% per year, for N years, in which case she'd have:
    A(1+I)N
    I say I% interest rate, but, if the rate were 8% per year, we'd use I = 0.08 in the following formulas, okay?
  2. Take your $D down payment and invest that at I% for N years, yielding D(1+I)N. Then take your monthly payments of $P and invest these at I% per year for N years ... or, let's say (I/12)% per month for 12N months. That'd yield P{(1+I/12)12N - 1}/(I/12) ... a magic formula - don't worry 'bout it. Finally, after N years she takes back the car whose residual value is, say, $R. The total dollars in the dealer's hand is (after N years) the sum:
    D(1+I)N + P{(1+I/12)12N - 1}/(I/12) + R
Okay. In order that the dealer make equal amounts for scenarios (1) and (2), the two final numbers (after N years) should be equal:

[**]       A(1+I)N = D(1+I)N + P{(1+I/12)12N - 1}/(I/12) + R

This allows us to determine the monthly payments $P ... uh .... well, let's simplify first:

We'll use an approximation for items like (1+I)N, namely 1+NI. Then the above equation becomes:

A(1+NI) = D(1+NI) + P{(1+NI) - 1}/(I/12) + R = D(1+NI) + 12PN + R

Notice that 12N monthly payments of $P turn out to be 12PN dollars. No compound interest with these approximations!

Okay, forging ahead, we solve for P like so:

P = (A - D - R)/12N + (A - D)I/12

  • The first term is the dealer's loss due to depreciation: she got $(A - D) from you, for the car, and after N years the car was only worth $R, for a loss of $(A - D - R) over 12N months, or $(A - D - R)/12N per month. This is called the Depreciation Fee.
  • The second term is what you're charged for interest on the loan: the dealer lent you $(A - D) to buy the car, at a rate of I/12 per month and that makes (A - D)I/12 monthly interest charges. This is called the Leasing Fee.

The spreadsheet uses something* like the above formula ... but I wouldn't count on your dealer using the same.

* The spreadsheet, and your dealer, actually uses a somewhat different formula: In the spreadsheet, the second "Leasing Fee" term is the average between (A - D)I/12 which is the monthly interest on the loan, and (R)I/12 which is the monthly interest on the residual value of the car. Their average is: (A - D + R)I/24 and the funny-factor I/24 is called the "Money Factor" (!)

That gives our final formula:

P = (A - D - R)/12N + (A - D + R)I/24
where (remember?):
  • N is the lease term, in years (so 12N is the number of months).
  • $A is the negotiated price of the car (after haggling).
  • $D is your trade-in or down payment (which may be $0).
  • $R is the residual value of the car: what it's worth after N years.
    It's a percentage of the Manufacturer's Suggested Retail Price (MSRP) and MSRP will usually be larger than $A, your price after haggling.
  • I is some annual interest rate: for 8.5% interest, put I = .085 in the formula.
  • (A - D - R)/12N is the Depreciation Fee (so the dealer recovers the depreciation after N months).
  • (A - D + R)I/24 is the Leasing Fee (to reflect the fact that the dealer is lending you money).
You can try this formula here:
Purchase Price of Car = $ that's A
Down Payment = $ that's D
Depreciated Value of Car = $ that's R
Number of Months = that's 12N
Interest Rate = % that's I%
Monthly Payments = $

If we use the magic formula [**] (without the simplications/approximations) we'd get monthly payments of:

P = (I/12) [(A - D)(1+I)N - R ] / [(1+I/12)12N - 1 ]

To use this formula, you can try this:
Purchase Price of Car = $ that's A
Down Payment = $ that's D
Depreciated Value of Car = $ that's R
Number of Months = that's 12N
Interest Rate = % that's I%
Monthly Payments = $

Some observations:

  1. You must add, to the monthly payments, any taxes (example 15% GST+PST, in Canada)
  2. The added taxes also apply to the Leasing Fee. (Surprise!)
  3. There may be freight charges, security deposit, acquisition fee, licence fee, etc.
  4. You'll have to buy liability insurance, maybe $1 million's worth.
  5. Normal wear and tear and mileage is assumed, when you return the car after N months ... else you'll pay extra.
  6. Early termination may be costly.
  7. The law requires that Capitalized Cost, Capitalized Cost Reduction, Residual Value, Lease Charges, Monthly Payments, and other amounts be clearly spelled out, in a uniform way (which bears little resemblance to English).

Okay, suppose:

  • You borrow umpteen dollars from the bank in order to buy a car outright: example $26000 ... the price of a car after trade-in?
  • After a certain number of months have passed you want to pay off the balance: example after 36 months ... the length of a lease?
  • The balance owed (to the bank) is some prescribed amount: example $15500 ... the value of the car when the lease expires?
  • You want to know what your bank payments would be.
The appropriate formula is:
P = [(A-D) (1+I)M/12 - R ] [(1+I)1/12 - 1] / [(1+I)M/12 - 1]

Use this:
Amount Borrowed = $ that's A - D
Months of Borrowing = that's M, the number of months (so M/12 = number of years)
Balance Owing = $ that's R, the residual value
Borrowing Rate = % per year that's I
Monthly Payments = $
Note that, here, we use (1+I)1/12 - 1 as the monthly interest (not I/12).
However, if we used that earlier approximation, replacing (1+x)n by 1+nx, then (1+I)1/12 - 1 = I/12

Note: The spreadsheet above has all three formulas.