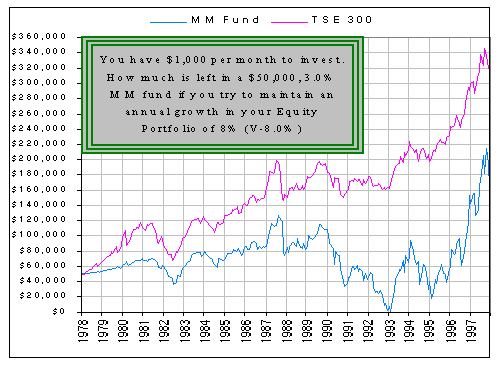
When the market don't go UP, the MM sho nuff go DOWN!
Note that the MM fund nearly ran out at the end of 1992 (which explains why I assumed $50K was originally in MM).
|
Date: 22-Jan-98 - 11:40 PM Subject: RE: Value Averaging vs DCA From: Jay Walker |
OK someone posted this title. What does "value" averaging mean, and how is it applied? (Is it based on market declines?)
Thanks
Jay
|
Date: 23-Jan-98 - 6:58 AM Subject: RE: Value Averaging vs DCA From: Bylo |
The term originates from the title of the book Value Averaging Michael Edelson, IPC ($22.95) on various strategies for investing lump sums of money among multiple assets based on market conditions. For instance, rather than DCAing a fixed amount each period, one invests larger amounts in down markets and less when they've gone up.
Haven't read the book (yet) nor is it listed in Amazon.
|
Date: 23-Jan-98 - 9:53 AM Subject: RE: Value Averaging vs DCA From: Bruce Cohen |
Value Averaging was published in 1991 by Michael Edleson, an assistant professor at the Harvard Business School. There were only two editions with small press runs and the book is extremely difficult to find in Canada.
I summarized Edleson's strategy and provided a sample spreadsheet in my book, The Money Adviser, which is published by Stoddart and available through any bookstore.
Edleson refined dollar-cost averaging to run an RRSP-type portfolio more like a traditional defined-benefit pension plan.. While DCA is focused on a set amount going in at fixed intervals, VA focuses on your progress toward a pre-established goal.
You start a VA plan by setting your target -- say $100,000 in 10 years -- and assuming average annual rates for growth and inflation. Say you assume you'll average 10% a year in growth with inflation averaging 2%.
Edleson recommends using one index equity fund and one money market fund. That's it. His formulas create a "value path" that shows where your account should stand at each month or quarter for you to meet your goal.
If the account balance is above that level, you transfer the difference from the equity fund to a money market fund. If it's below, you top up the equity fund with cash from the MMF or new money. The decision is automatic, based on your pre-plotted value path, not your assessment of the market.
The key point to understand is that this plan is for disciplined, conservative investors because it essentially caps your long-term growth at the rate originally assumed. Therefore, when stocks fly high, you will be largely in cash. You can relax in the feeling that you're on target for your plan but you must be willing to sacrifice bragging rights.
|
Date: 23-Jan-98 - 1:39 PM Subject: RE: Value Averaging vs DCA From: Jay |
Does it provide a superior return to DCA?
|
Date: 23-Jan-98 - 2:40 PM Subject: RE: Value Averaging vs DCA From: Bylo |
Jay,
Well according to Mr. Cohen's book "Edelson ran hundreds of tests using US stock market data from 1926 to 1991 and found VA beat DCA more than 90% of the time." pp253-254
|
Date: 24-Jan-98 - 1:09 PM Subject: RE: Value Averaging vs DCA From: gummy |
I don't really understand Value Averaging, but I think it's something like this:
You have $1K per month to invest and, say, $50K in Money Market.
You want to achieve an annual gain of, say, 8%, in your Equity Portfolio.
If, at the end of each month, your Equity Portfolio increases at the 8% rate (... whatever that turns out to be, monthly) you're happy so put your $1K into Money Market instead (which grows at some rate, say 3%/year).
If your portfolio increases by less than the 8% rate, you put into your Equity Portfolio whatever is necessary from your $1K and your MM fund in order to achieve the required growth rate.
If your portfolio increases by more than the required rate, you're ecstatic and you not only put your $1K into your MM fund, you also withdraw from your Equity Portfolio whatever is necessary to reduce the growth rate to 8% per year.
Is that the algorithm? If not I'll call it V-8% (instead of Value Averaging).
I had some difficulty keeping the required growth rate (8%) low enuff ... and the initial MM fund large enuff ($50K)... to avoid running out of MM funds!@$#%
Here's what happens to the balance in the MM fund (where I show the growth of the TSE, for comparison):

When the market don't go UP, the MM sho nuff go DOWN!
Note that the MM fund nearly ran out at the end of 1992 (which explains why I assumed $50K was originally in MM).
Here's the V-8% portfolio (the initial MM fund + monthly additions) compared to just investing all $50K MM and DCAing $1K/month
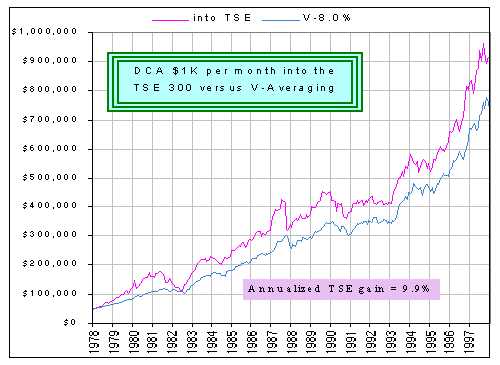
Note that both start with the $50K.
|
Date: 24-Jan-98 - 4:09 PM Subject: RE: Value Averaging vs DCA From: Jay |
Gummy, can you project what would happen to a portfolio requires a return rate IN EXCESS of the average TSE return (say 12%, since the rate here is 9.9%)? Is it actually achievable, or do you end up with all the funds always going in the market in a futile attempt to exceed the benchmark?
|
Date: 24-Jan-98 - 4:38 PM Subject: RE: Value Averaging vs DCA From: gummy |
Jay: I actually started with a "required" return of 10% (doesn't everybuddy use that number?) and found that, unless you had a $150,000 cushion in Money Market, you'd run out of money there!@#$
I'll do it more carefully and let you know.
(Personally, I don't understand the logic behind "Value Averaging". If I had that much money in MM to start with, I'd want to get it into the market!)
|
Date: 24-Jan-98 - 5:47 PM Subject: RE: Value Averaging vs DCA From: gummy |
Here's what happens if you "ask" for more than the market can provide:
The TSE 300 had an annualized return of 9.9% over the past 20 years (ending Dec 31/97).
You want to "Value Average" (if that's what it is) to get an annualized return of 12% (greedy! greedy!).
You'll need $156,000 in a 3% Money Market fund (else you won't be able to top up your Equity Portfolio).
Your Equity Portfolio will grow exponentially (see the smooooth graph, below) at 12%/annum.
Your MM fund will go to almost zero at the end of 1994 (and that's why you needed $156K).
The TOTAL of your Equity Portfolio and your MM fund is also shown (that's V-12%), as well as what you'd have if you just put everything ($156K + $1K/month) into the TSE 300.
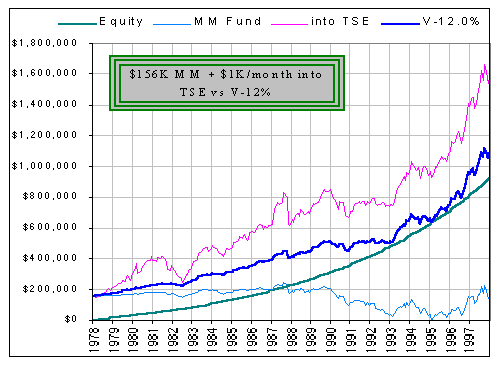
There's no argument. You DO make 12% in your Equity Portfolio.
Aah, but y'all got thet thar $156K setting in MM at jest 3% .
|
Date: 24-Jan-98 - 10:53 PM Subject: RE: Value Averaging vs DCA From: Jay |
Gummy, possibly there's something more to this since Bylo reports (according to Cohen's book) that Value Averaging beat DCA over 90% of the time. (also, the full name of the book is "Value Averaging: The safe and easy strategy for HIGHER Investment Returns)
I went down to my local bookstore, and they are going to call their people regarding Value Averaging to see if it is available. They show it on their computer system, so if it's still available I'll get a copy and let you know.
Till then,
Cheers!
Jay
|
Date: 24-Jan-98 - 11:08 PM Subject: RE: Value Averaging vs DCA From: Jay |
Went surfing (let's go surfing now everybody come on ...) and found this ...
I think I understand it now.
|
Date: 24-Jan-98 - 11:11 PM Subject: RE: Value Averaging vs DCA From: Jay |
Boy is the librarian going to be mad.
|
Date: 24-Jan-98 - 11:12 PM Subject: RE: Value Averaging vs DCA From: Jay |
Whew! Fixed it!
|
Date: 24-Jan-98 - 11:40 PM Subject: RE: Value Averaging vs DCA From: Jay |
Here's something else explaining it, together with a claim that it outperforms DCA by about 2% (unknown time frame, US market assumed?) ...
"Value averaging is a strategy in which a person adjusts the amount invested, up or down, to meet a prescribed target. An example should clarify: Suppose you are going to invest $200 per month in a mutual fund, and at the end of the first month, thanks to a decline in the fund's value, your $200 has shrunk to $190. Then you add in $210 the next month, bringing the value to $400 2*$200). Similarly, if the fund is worth $430 at the end of the second month, you only put in $170 to bring it up to the $600 target. What happens is that compared to dollar cost averaging, you put in more when prices are down, and less when prices are up.
Dollar-cost averaging takes advantage of the non-linearity of the 1/x curve (for those of you who are more mathematically inclined). Value averaging just goes in a little deeper when the value is down (which implies that prices are down) and in a little less when value is up.
An article in the American Association of Individual Investors showed via computer simulation that value averaging would outperform dollar- cost averaging about 95% of the time. "Outperform" is a rather vague term. As best as I remember, whatever the percentage gain of dollar- cost averaging versus buying 100% initially, value averaging would produce another 2 percent or so."
Which came from this site The Investment FAQ
Till later,
Cheers!
Jay
|
Date: 24-Jan-98 - 11:46 PM Subject: RE: Value Averaging vs DCA From: Matador |
Great info Gummy.
A meaningful chart is worth 100 threads.
Keep up the good work!!!
|
Date: 24-Jan-98 - 11:47 PM Subject: RE: Value Averaging vs DCA From: Matador |
Great info Gummy.
A meaningful chart is worth 100 threads.
Keep up the good work!!!
|
Date: 24-Jan-98 - 11:47 PM Subject: RE: Value Averaging vs DCA From: Matador |
Great info Gummy.
A meaningful chart is worth 100 threads.
Keep up the good work!!!
|
Date: 25-Jan-98 - 5:35 AM Subject: RE: Value Averaging vs DCA From: gummy |
Jay: I went surfing.
AHA! I knew there was a good reason for my avoiding the term "Value Averaging" (and using V-8 and V-12 instead, like some hi-powered car). The scheme I considered was not "Value Averaging".
(Maybe it was "Gummy Averaging" ... which explains why it's a lousy scheme).
In "Value Averaging" you ask for a FIXED DOLLAR increase each month, not a FIXED PERCENTAGE increase. That gives me something else to work on ... I'll be back ...
P.S. Jay: y'all probably know that it's yer TSE data thet gits fried 'n masticated here.
|
Date: 25-Jan-98 - 7:26 AM Subject: RE: Value Averaging vs DCA From: gummy Can anyone explain to me how the "Total Amount Invested" is $12,000 (for DCA), in the table at: Ain't it $10,000?
Folks, Cohen's book includes a VA spreadsheet. When I get back to town next weekend (I'm freezing my butt right now here in Orlando) I'll post it here.
I've got Jay's 1960 to 1997 TSE 300 data embedded in a VA spreadsheet (with Sexy Pictures*), but before I post them I'll wait for a Bylo/Cohen spreadsheet (so ah don't make me-self foolish, jest in case ah done got it wrong). BUT, it seems (at first blush) that VA has the following characteristics:
Aw shucks ... I stuck my VA stuff into my gummy_stuff website anyhow (even if it is wrong). Funny thing about the VA examples I've seen. It's assumed you look at the closing price, then you do your calculations, then you invest whatever is necessary to achieve the fixed dollar increase ... and you buy at that closing price!?!?
With any luck, this should be a tie-in to the appropriate Amazon page for the Value Averaging book ... Value Averaging Page at Amazon I hope ... Cheers! Jay
Why not DCA and lump sum during corrections, like I'm sure a lot of FundLib folks did in late Oct-Nov 97.
gummy, Haven't forgotten 'bout the spreadsheet. I'll do that later today or tomorrow. Jay, Thanks for the Amazon reference. Now I understand why I couldn't find it before -- my search was by Title and Author (Edelson), but the actual entry does not include the latter. :-(
Once-upon-a-time I thought Value Averaging was designed to achieve a fixed percentage growth each month in your Equity Portfolio ... like, maybe, 1%. We set a goal for N months from now, say $A. That's P(N), the value of our (Equity) Portfolio after N months.
|