| Dimensionless Financial Ratios: a continuation of Part I |
| some Stock Comparisons |
In Part I we considered the standard P/E and PEG Ratios, namely:
P/E Ratio = (stock Price) / (annual Earnings per share) which is measured in years
PEG Ratio = (P/E Ratio) / (Earnings Growth Rate) which is measured in years2
... and various modifications.
Here we'd like to compare a few stocks, using the modifications we introduced, namely:
the M/E Ratio
and the dimensionless ratios gPEG,
gNUM and gRANK, where:
|
M/E Ratio = EV / EBITDA years
gPEG = PEG(stock) / PEG(index) gNUM = PEG * Volatility2 gRANK = M/E * Volatility2 / (Earnings Growth Rate) |
>Can you find the data?
Not easily

>How about starting with the DOW 30?
I'll give it a try. First we need the PEG of the DOW (to compute gPEG), using:
|
PEG(DOW) =
(M1+M2+ ... +M30) /
( r1E1+ r2E2+ ... + r30E30) years2
where the Ms are the market caps (in dollars) and the rs are the earnings growth rates (per year) and the Es are the total company earnings (in dollars per year) |
We get (I think!):
- M1+M2+ ... +M30 = 3031.6 billions of dollars
- r1E1+ r2E2+ ... + r30E30 = 9.212 billions of dollars per year2
- Then PEG(DOW) = 3031.6 / 9.2121 = 329.1 year2
Yeah, maybe because we've included all those negative earnings ... and that'd make that 9.212B pretty small

Then, for the 30 components of the DOW, we'd get (for sometime-in-December, 2003):
| Stock | P/E | PEG | M/E | 1000gPEG | gNUM | gRANK | Stock | P/E | PEG | M/E | 1000gPEG | gNUM | gRANK | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GE | 20.9 | 1.9 | 24.1 | 5.6 | 1380 | 5607 | MSFT | 28.6 | 2.2 | 17.4 | 6.7 | 5084 | 1443| WMT | 27.3 | 1.7 | 14.3 | 5.2 | 1374 | 562 |
| C | 15.9 | 1.2 | ?? | 3.5 | 886 | ?? | XOM | 13.6 | 1.9 | 6.5 | 5.7 | 488 | -66 |
| INTC | 50.2 | 2.7 | 30.7 | 8.3 | 12096 | 962 | IBM | 23.4 | 2.1 | 13.4 | 6.4 | 2808 | -331 |
| JNJ | 21.9 | 1.4 | 12.2 | 4.4 | 793 | 410 | PG | 24.8 | 2.0 | 14.0 | 6.1 | 2163 | 789 |
| KO | 26.7 | 2.4 | 18.7 | 7.3 | 1540 | -520 | MO | 12.0 | 1.3 | 8.2 | 3.8 | 1603 | 351 |
| MRK | 14.0 | 2.0 | 9.4 | 6.0 | 1716 | -4566 | HD | 20.6 | 1.4 | 12.9 | 4.2 | 2042 | 935 |
| SBC | 10.4 | 7.5 | 5.8 | 22.8 | 8983 | -316 | JPM | 16.6 | 1.2 | ?? | 3.5 | 2132 | ?? |
| HPQ | 27.2 | 1.5 | 17.2 | 4.4 | 4778 | -175 | MMM | 28.0 | 2.2 | 14.6 | 6.6 | 930 | 164 |
| AXP | 20.5 | 1.5 | 15.6 | 4.6 | 1308 | 129 | DIS | 35.0 | 1.8 | 24.1 | 5.3 | 2120 | ?? |
| DD | 60.3 | 3.0 | 20.4 | 9.1 | 2071 | -112 | UTX | 19.2 | 1.8 | 10.0 | 5.6 | 2243 | 794 |
| MCD | 32.6 | 2.2 | 12.6 | 6.8 | 2398 | -296 | BA | 183.3 | 4.0 | 17.7 | 12.2 | 6596 | -353 |
| AA | 32.2 | 2.0 | 12.0 | 6.2 | 3326 | -365 | CAT | 25.0 | 2.3 | 15.3 | 6.8 | 2626 | -19847 |
| HON | N/A | 1.9 | -201.7 | 5.8 | 5495 | ?? | GM | 6.4 | 1.4 | 19.9 | 4.1 | 2042 | 159 |
| IP | 139.7 | 7.1 | 13.3 | 21.5 | 7316 | ?? | T | 17.7 | -0.5 | 3.5 | -1.5 | -2026 | -54 |
| EK | 19.1 | 2.3 | 6.4 | 6.9 | 4704 | 14 | |
Because we're dividing by that big PEG(DOW) which makes gPEG uncomfortably small.
>But the "best" PEG is also the "best" gPEG!
Uh ... yes, it is, isn't it?
>It's so confusing! All those ??
Some of the data I haven't found, yet (hence the ??) and some Earnings and Earnings Growth were negative and ...
>It's confusing! We're looking for the smallest value ... but which one?
Take your pick. Here's the "best", ignoring those "??" and negative values:
| Rating | P/E | PEG | M/E | gPEG | gNUM | gRANK |
| Best | GM | C | T | C | XOM | EK |
>So are you happy?
I'm not convinced that the numbers are correct ... so I'm not happy (yet).
>The numbers for GE and MSFT don't even agree with Part I !
Yeah ... I'm still working on that ... but the numbers change from day to day, eh?
>So what's the "best"? I mean, what should I buy?
I'll let you know in a few months

>Haven't you tried to pick winners before? I remember your gummy bears.
Yeah, don't remind me. That was 2 or 3 years ago. I picked EK (Eastman Kodak) and T (AT&T). Since then they've both had annualized returns of about -20%.
>You're not very good at this, are you?
Don't remind me.
There's a .ZIPd spreadsheet ... such as it is!
I wouldn't trust it, but it's fun to play with and, of course, there's a money-back guarantee
Just RIGHT-click here and Save Target ... file.
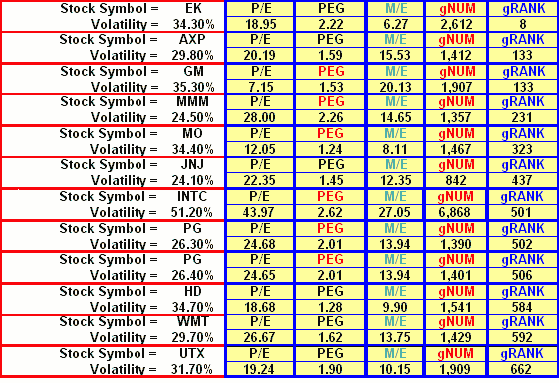
It'll compare two stocks, giving something like this:

>Volatility? Where would I get those?
Uh .. you could try the spreadsheet described here