At the end of the first month the amount we owe is now B(1+R) so we make our first payment of $P,
leaving a balance owing of B(1+R) - P.
To make things look simpler, we'll let (1+R) = x, so the balance in our mortgage (after one month) is Bx - P.

After another month this balance has grown by a factor (1+R) = x,
so it's now (Bx - P)x but then we make another payment of P
leaving a balance of Bx² - Px - P.

Okay, one more time (then we'll see the pattern):
Another month goes by and the balance of Bx² - Px - P increases by a factor x again,
and we make another $P payment leaving a balance of
Bx³ - Px² - Px - P.

After N months, the balance owing is:

Bx^N - P(x^N-1 + x^N-2 + ... + x + 1).

As you might imagine, there's a magic formula:
x^N-1 + x^N-2 + ... + x + 1 = (x^N - 1) / (x - 1)
so the balance after N months (and N payments) is:
Bx^N - P(x^N - 1) / (x - 1)
and, if it's an N-months mortgage (meaning it's all paid off after N months), then the balance is zero, so:
Bx^N - P(x^N - 1) / (x - 1) = 0
and now we can determine the monthly payments
... but it's time to replace x by (1 + R) again,
so we solve for P and get:

[!]    P = BR/ (1 - (1 + R)-N)

The last problem is to determine R, the monthly mortgage rate. If the annual rate is Q, then, for a Canadian mortgage (which involves the peculiar phrase half yearly rests), the six-month rate is Q/2 and the monthly rate of R, compounded for 6 months must give Q/2 so (1 + R)⁶ = 1 + Q/2 and that gives us:

R = (1 + Q/2)1/6 - 1

You supply the value of B and N and Q and the spreadsheet calculates
R and the monthly payments and the balance after each payment, etc.

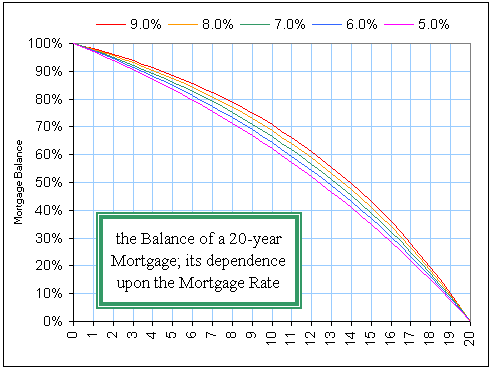
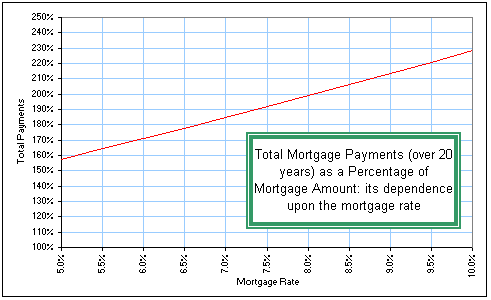
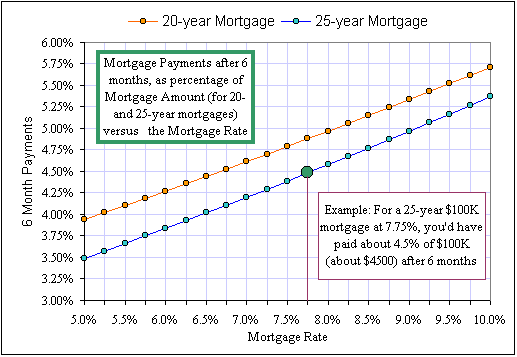
Here's a BETTER spreadsheet to play with:

Just RIGHT-click on the picture and Save Target to download a .ZIPd spreadsheet.
It calculates a bunch of stuff (Canadian or U.S. mortgages) and compares two mortgages with different parameters.