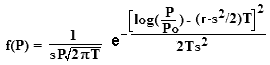Portfolios
Once upon a time I wrote a tutorial on Ito calculus (summarized here).

One of the interesting results was the distribution of stock prices after T years (starting, for example, with a $1.00 stock price). For example, with a Mean Return r = 10% and a Standard Deviation s = 20%, Figure 1 illustrates the magic formula for the distribution after T = 2 years, 4 years etc.

>So?
Well, I thought it'd be fun to see what we can do with that formula.

>Didn't you get the Black-Scholes option premium?
Well, yes, I regurgitated what I had read ... but maybe we can do something else.
If you KNEW the distribution of stock prices one year from now, how would you use that information?


Figure 1
>Wow! If I knew the stock price one year from now I'd ...
No! Not the price! The distribution of prices!
However, suppose:
  • We start with N(0) shares of stock at P(0) = $1.00   ... our portfolio is worth N(0)P(0).
  • In T = 1 year we have N(1) shares, worth P(1)   ... our portfolio is worth N(1)P(1).
  • In T = 2 years we have N(2) shares, worth P(2)   ... our portfolio is worth N(2)P(2).
  • etc. etc.
  • In T years we have N(T) shares, worth P(T)   ... our portfolio is worth N(T)P(T).
  • Now suppose that, at year t (including t = 0), we buy a fixed $A worth of stock   ... that's like Dollar Cost Averaging, eh?
  • At P(t) dollars per share, that means A/P(t) shares purchased   ... to be added to the shares already owned.
  • That means that the number of shares owned at time t is: N(t) = N(t-1) + A/P(t)   ... adding the newly purchased shares.
  • Starting at t = 0, the number of shares owned at time T is then: N(T) = A/P(0) + A/P(1) + ... + A/P(T).
  • That means that the value of our portfolio at time T is: N(T)P(T) = A P(T)[1/P(0) + 1/P(1) + 1/P(2) + ... + 1/P(T)].
>That looks vaguely familiar. Haven't you ...?
Yes. It's related to our magic sum. However, we want to do something different this time. In fact, we'd like to look just one year into the future, then invest or withdraw from our portfolio, then look again just one more year into the future, then invest or withdraw, then ...

>Yeah, so?
So we need to do some preliminary work:

Let's just look at the (original) Ito formula, namely

... but after T = 1 year where we put P(0) = $1.00
and set P/Po = G (the one-year Gain Factor).

A sample distribution is shown in Figure 2.


Figure 2
A point to remember: The Ito formula gives a lognormal distribution of gain Factors.

Now, you'd think that the Gain Factor over n years could be generated by applying the 1-year Gain Factor n times, eh?
That means that we'd pick, at random, a 1-year Gain Factor G1 from the distribution in Figure 2, then another 1-year random Gain Factor G2 (from the same distribution), then we'd ask for the distribution of G1G2.

Let's assume that the Mean and Variance of the G-distribution (that's the distribution of 1-year Gain Factors) are M[G] and V[G] respectively.

Now, assuming that the selection of the Gain Factors G1 and G2 are uncorrelated, we can use stat-stuff#10 to get the Mean and Variance of the distribution of 2-year Gain Factors: G1G2, namely:
[1]       M[G1G2] = M2[G]
[2]       V[G1G2] = 2M2[G]V[G] + V2[G]

The notation M[G] and V[G] is to cumbersome, so we'll just use M and V and rewrite [1] and [2] like so:
[1A]       M[G1G2] = M2
[2A]       V[G1G2] = 2M2V + V2

Now, since the distribution of G1G2 is lognormal with Mean and Variance given by [1] and [2],
we know that it has the form eg where g has a normal distribution and ...

>Huh?
That's the definition of a lognormal distribution.
G has a lognormal distribution if each G-value is eg where g has a normal distribution.

Our problem, then, is to find the Mean and Variance of the set g (which is, we see, the logarithm of G1G2).

>So, if G is lognormal, then log(G) is normal, right?
Right, except we're now talking about the 2-year Gain Factor G1G2.
Now, to get the Mean and Variance (or StandardDeviation2) of the normal set g = log(G1G2), namely M[g] and V[g], we use the stuff here to get:
[3]       V[g] = SD2[g] = log(1 + V[G1G2] / M2[G1G2]) = log(1 + 2V + V2 / M2)     dividing 2A by 1A
[4]       M[g] = log(M[G1G2]) - V[g] = 2 log(M) - log(1 + 2V + V2 / M2)     using 1A and 3

Now we have the Mean and Variance (or SD2) for our normal distribution.
That means that g = log(G1G2) has a normal distribution so that ...
>Remind me. What's a normal distribution?
It's defined here in Figure 2

Okay, putting it all together, we have that g = log(G1G2) = log(2-year Gain Factor) has the normal distribution:

EXP[-(1/2)(g-M[g])2/SD2[g]] / (SQRT(2π)SD[g])

If f(x) is a normal density distribution for X,
with Mean = m, Standard Deviation = S,
then
   
meaning:
the probability that X lies in [x,x+dx] is f(x)dx.

Figure 2
Consider just the exponent: {(g-M[g])/SD[g]}2 = {g-2 log(M) + log(1+2V+V2/M2)}2 / log(1 + 2V + V2)