Here's what we want to do:

Download ten years worth of daily prices for some stock, say GE. Generate a distribution of daily returns, like Figure 1. Apply this distribution of returns to a fictitious stock whose current price is, say $10.     This fictitious stock has nothing to do with GE stock.     Its evolution in time just uses the GE return distribution. Pick a number of days into the future, say 30. Select 30 returns at random, from the return distribution (as in Fig. 1). See what happens to your $10 stock, after 30 days. Repeat steps 5 and 6 a jillion times and generate a probability distribution of prices, 30 days in the future.

Figure 1

>And that's exact? Are you kidding? To be exact you'd need this. It's an estimate of a future stock price assuming the historical return distribution of GE stock is relevant. Now that you have an estimate ... >Is there a spreadsheet? Yes. Patience! Having an estimate of a future price such as Figure 2, you might use it to estimate the value of a stock option, for example. In Fig. 2, the red dot is the current price that you've entered. >Options? Black-Scholes says: Call Premium = S*NORMSDIST((LN(S/K)+(R+V^2/2)*T)/(V*SQRT(T))) - K*EXP(-R*T)*NORMSDIST((LN(S/K)+(R+V^2/2)*T)/(V*SQRT(T))-V*SQRT(T))

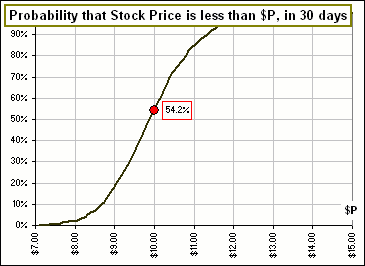
Figure 2

>Huh?
The various parameters involved are explained here and ...

>And the spreadsheet?

>That's so confusing that ...
There's an Explain sheet which looks like this.

>What about that option stuff? Yeah, it's there, too ... and looks like this: You stick in the Strike Price etc. and it calculates the option premium (a la Black-Scholes). You also get the probability of achieving some Wished-for Stock Price. In Fig. 3, that's the Break-even stock price, namely Strike + Premium ... and the probability of achieving this in 30 days is 34.7%. >And that's exact? Of course! Would I lie to you?

Figure 3

for Part II