I got email from Ron McEwan about generating ellipses that contain points in a scatter plot where ...

>Wait! What are you talking about?
Okay, we do this:

Plot a bunch of points (x1, y1), (x2, y2) ... (xn, yn)   (that's our scatter plot) Generate an ellipse centred on the origin. Vary the lengths of the axes to that it'll contain "most" of the points. >Most? Okay, let's do this: Assume we have stock returns for two stocks: pk and qk for k = 1, 2, ... n. Assume that they are random selections from some distribution. We plot the deviations from the Means. That is, if M[p] = (p1 + p2 + ... pn) / n, then we actually plot xk = pk - M[p]. Do the same for the y-values. That is, plot yk = qk - M[q]. Note: The origin (0,0) represents a point where both returns are at their respective Means.

Fig. 1   Ellipse and scatter plot

If the returns have a normal distribution, then each set of x- and y-values has Mean = 0 and, let's say, Standard Deviations Sx and Sy. Then there's a probability of finding the x-value between x and x + dx given by the magic formula Similarly for y values, so we imagine a wee rectangle and ... >Rectangle? Can you see that wee rectangle in Figure 1? The width is dx and the height is dy and it's located at (x,y). >I really think that ...

Fig. 2 Normal distribution: (zero mean) f(x) dx is the probability of x being in an interval about x of width x

Patience. All will be clear in a minute or three.

Okay, knowing the probability of the horizontal value being in a wee interval at x and the vertical value being in a wee interval about y, the probability of finding a point in a wee rectangle at (x,y) should be (using the magic formula in Fig 2) proportional to:

e-(1/2) { (x/Sx)2 + (y/Sy)2}

For sanitary reasons, we'll let Sx = a and Sy = b so we get:

e-(1/2) { (x/a)2 + (y/b)2}

>You just multiply the probabilities, right?
Yes, that's what I've done.

Then there are curves where the probability is constant, namely ... >Don't tell me! They're the curves (x/a)2 + (y/b)2 = constant. Indubitably! And those curves have a name. They're called ... >Don't tell me! They're ellipses. You got it. Okay, now comes the interesting part ... rotating the ellipse. >And the significance of that is ... what? Patience.

Fig. 3   A rotated ellipse

Let's look at a real, live scatter plot, say GE versus the DOW Fig. 4 show the relationship between the daily returns, over the past year. See the four wee rectangles? According to the above prescription, we should associate with each the same probability, but we see that ... >But the rectangles in the 2nd and 4th quadrant don't have too many points. In fact, the points seem to ... They seem to crowd together along the "regression line", right? (See this or this.) So, if the returns are not independent, but somehow tend to be linearly related (as implied by their hugging the regression line), then the prescription above for the probability of finding a point in a wee rectangle needs to be modified. Indeed, if we have a randomly selected x-value, the corresponding y-value is likely to be close to that regression line. If the equation of that line is y = mx + k, then for a given x-value, we expect the y-value to be close to mx + k.

Fig. 4   GE returns vs DOW returns

>What's that tall skinny rectangle doing in Fig. 4?
Patience. By the way, if you want to see a scatter plot where the returns really hug the regression line, check this out:

Okay, we'll study Bayes Theorem. It gives us the probability of getting a particular pair (x,y) if y depends (in some way) upon x.

We'll call P[x] the probability of getting a particular x-value. (Actually, P[x] will be the probability of getting a value in some wee interval about x.)
The probability of getting a particular y-value given that x-value is (according to Bayes):

[A]     P[x and y] = P[x] P[y, given x]

The guy called P[x] can be obtained from Fig. 2 (assuming the x-values are normally distributed):

[B]     P[x] is proportional to e-(1/2) (x/a)2

To get P[y, given x] we have to stare carefully at the distribution of y-values for a given x-value. (Remember the tall, skinny rectangle?)
Since we're doing the math snow-job thing (by assuming normal distributions for convenience simplicity), we'll assume that the y-values are normally distributed about mx + k.
(Them's the y-values in the tall, skinny rectangle in Fig. 4 ... distributed about the value mx + k).
That is, the probability P[y, given x] looks like what's in Fig. 2, with x replaced by y - mx - k:

[C]     P[y, given x] is proportional to e-(1/2) {(y - mx - k)/c}2   where c is the standard deviation associated with the distribution of y-values for a given x-value.

>Huh? Replace y by y - (mx + k)? Can you do that? In Fig. 2, the variable x appears all by itself 'cause its mean is 0.   In general (for a non-zero mean), we'd have this

In our investigation of the distribution of y-values, given x, the Mean value of the y-values is assumed to be (mx + k).

>Can you do that?
This is mathmanship, remember?

Now we plug [B] and [C] into [A] and get something that looks like this:

[D]     P[x and y] is proportional to e-(1/2) (x/a)2e-(1/2) {(y - mx - k)/c}2

>But I don't see any characteristics of the y distribution. I mean, where's the standard deviation of the y-values and ...
They're tied up in the values of m and k. Just wait until we're finished, okay? All will become clear.
>I doubt it!

Okay, we stare at [D] and see that the curves of constant probability look like: [E]     (x/a)2 + {(y - mx - k)/c}2 = constant >Aha! That's a rotated ellipse, right? How would I know? >But that ellipse lies along the regression line, right? How would I know?

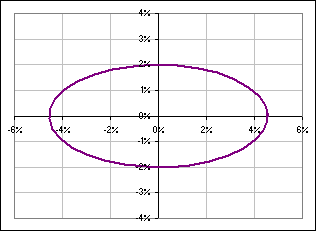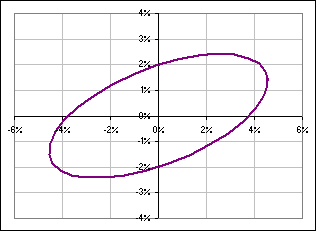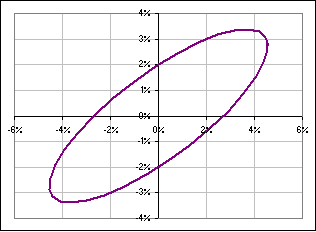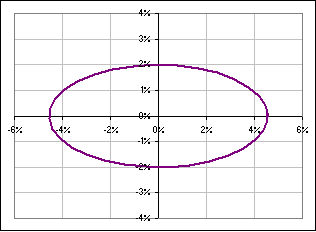Fig. 5a   (x/a)2 + {(y - mx - k)/c}2 = 1 with varying m

Fig. 5b   GE and DOW and an ellipse

>Okay, but you said that the y-values are normally distributed ... in that tall, skinny rectangle. Is that true? You kidding? Of course it's true! Take a look at the daily returns on GE over the past 8 years, when the DOW had returns between 1.0% and 1.5%. (That is, the width of that skinny rectangle is 0.5%). Now look at the distribution of GE returns for that range of DOW returns. It's a perfect normal distribution:

Fig. 6   GE distribution

>So, where's the spreadsheet?
Click on the picture:

>Uh ... is it useful?
How would I know?