Here's the problem:

Does Σ cos(n)/n converge ... where the sum is from n = 1 to n = ∞?

>Lookin' at Figure 1, I'd say yes. Can you prove it? >Me? You kidding? Let's try. There's a test for convergence due to Dirichlet that says: If the sequence an is decreasing and has a limit of 0 and the sum |Σbn| is bounded then Σanbn converges. >I pick an = 1/n because it decreases to 0. Right? Yes, and I'll pick bn = cos(n). >Then you gotta prove that Σ cos(n) is bounded.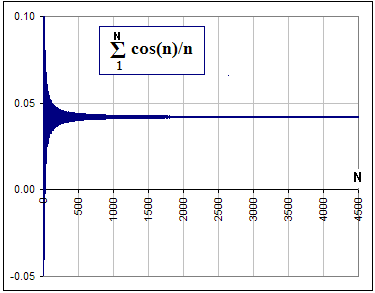

Figure 1

Recall that eⁱⁿ = cos(n) + i sin(n).
Then Σ eⁱⁿ = Σ cos(n) + i Σ sin(n).
But Σ eⁱⁿ is a geometric series with a common ratio of eⁱ so its sum (from n = 1 to n = N) is:   eⁱ(1 - e^iN) / (1 - eⁱ)

>Huh?
Remember? a + ar + ar² + ... + ar^N-1 = a (1 - r^N)/(1 - r). In our case, a = r = eⁱ.
Okay, so what's an upper bound on |Σcos(n)| ?

>I give up.
|Σcos(n)| < |Σ cos(n) + i Σ sin(n)| = |Σeⁱⁿ| = |Σ eⁱ(1 - e^iN) / (1 - eⁱ)| < |eⁱ||1 - e^iN| / |1 - eⁱ| < 2/|1 - eⁱ| = 1/SQRT[1 - cos(1)]
since 1 - eⁱ = 1 - cos(1) - i sin(1) has a magnitude of SQRT[(1 - cos(1))² + sin²(1)] =SQRT[ 2 - 2 cos(1)].

>Okay, so Σ cos(n)/n converges ... but to what?
I have no idea.

Mark S. provided this neat result:

Note that (Taylor series, eh?):
Σxⁿ/n = -log(1 - x).

Setting x = eⁱ we get:
Σxⁿ/n = Σeⁱⁿ/n = -log(1 - eⁱ).

Then Σcos(n)/n = -RealPart{ Σeⁱⁿ/n } = -RealPart{ log(1 - eⁱ) }

But the log of a complex number R e^iθ is just log(R) + iθ so the RealPart is just log(R).

Note that: 1 - eⁱ = 1 - cos(1) - i sin(1) = R e^iθ with R = SQRT[ (1 - cos(1) )² + sin ²(1) ] = SQRT[ 2 - 2 cos(1) ].

So (finally): Σ cos(n)/n = - log(R) = - log[ SQRT[ 2 - 2 cos(1) ]] = 0.04202.

>Just like Figure 1, eh?
It looks that way, don't it.

See Math Stuff