If dP = μdt + σdx, then:
      ΔP = μΔt + σΔx
      ΔP² contains terms involving Δt², ΔtΔx and Δx²
      Let Δx and Δt 0
      Put (in the limit) ΔP² = dP², Δx² = dx² = dt, ΔxΔt = 0, Δt² = 0
      Get dP² = σ²dx²

Moral? Whenever we see dP² we can replace it by σ²dx² ... or even σ²dt  

That gives us:

[Ito's Lemma]       If P(t,x) follows a stochastic process, described by                 dP = μ(t,P)dt + σ(t,P)dx                 and x(t) is a Brownian Motion (so, among other things, dx2 = dt)                 then F(t,P) satisfies:                 dF = Ft dt + FP dP + (1/2) FPP dP2 = [FPμ + Ft + (1/2)FPPσ2]dt + FPσdx

We're going to model stock price evolution via:

[Ito*]       If r is the Mean Return and s is the Standard Deviation, then we assume that changes in Price satisfy:                 dP = r P dt + s P dx, with solution:                 P(t) = P(t0) exp[(r-s2/2)(t-t0) + s (x(t)-x(t0))]                 where x(t) is a Brownian Motion with a Normal density distribution described by:                 G(u) = 1/SQRT[2πT] EXP[- u2/2T] with T = t - t0.                 meaning that the probability that X(t) = x(t) - x(t0) lies in [u,u+du] is G(u) du.

Note that, for a Normally distributed random variable X ...

[Normal] If f(x) is a normal density distribution for X, with Mean = m, Standard Deviation = S, then meaning: the probability that X lies in [x,x+dx] is f(x)dx.

Let's continue ...
The prescription dP(t) = {r dt + s dx(t)}P(t) describes a so-called Geometric Brownian Process (a special, restricted case of the more general stochastic process described in Ito's Lemma, above).
>So that's an assumption ... that stock prices follow a Geometric Brownian Process?
Yes. In particular, note that, if we put X(t) = x(t) - x(t₀) and T = t - t₀, so that P = Po exp[(r-s²/2)T + s X],
then we can solve for X = (1/s) [log(P/Po) - (r-s²/2)T] ... and this expression will come back to haunt us.

Indeed, the density distribution for P, meaning the probability that P will lie in [u,u+du], is
[-1]    G(u) = 1/{s u SQRT[2πT]}   EXP[- X²/2T] = 1/{s u SQRT[2πT]} EXP[- {log(u/Po) - (r-s²/2)T}²/2Ts²]

Here, we've put X = (1/s) [log(P/Po) - (r-s²/2)T] and, in the Normal prescription, Standard Deviation = s SQRT(T). (We'll return to this in [4], below.)

Now we want to concentrate on something like the price of an option which, of course, depends upon the underlying stock price, P(t).

To this end we consider a function F(t,P) which depends upon P(t,x).
Using Ito's lemma (for the special case of our Geometric Brownian Process), and noting that
μ(t,P) = rP and σ(t,P) = sP, we get:

[0] For F(t,P) where P(t,x) is a Geometric Brownian Process with x(t) a Brownian Motion: dF = Ft dt + FP dP + (1/2) FPP s2P2dt     ... that's Ito's Chain Rule       = [FPrP + Ft + (1/2)FPPs2P2]dt + FPsPdx     ... substituting for dP

In this formula, the fact that dx² = dt was used.
>Obviously. I knew that because ...
Pay attention.
If we should happen to find some variable, C, which satisfies an equation like:
            dC = A C dt + B C dx with x(t) Brownian,
then C would follow an Ito process, as in [Ito*], where A is the Expected value of changes in C (that's dC) and B² is the Variance of these changes. In a minute, C will be the value of our Call Option. It clearly depends upon the stock price P, and P is an Ito process (with constant r and s), and we'll find that C is also an Ito process ... with more complicated Expected values for changes and Variance.

>In a minute? Why wait ... ?

Okay, let's consider the value of a Call Option, C = C(t,P) where P = P(t,x) is a Geometric Brownian Process which satisfies [Ito*]. Using [0], we can find the differential of such an animal:
            dC = C_t dt + C_P dP + (1/2) C_PP s²P²dt = [C_PrP + C_t + (1/2)C_PPs²P²]dt + C_PsPdx
which we recognize as having the form:
            dC = A C dt + B C dx
where
[!!]            A C = [C_PrP + C_t + (1/2)C_PPs²P²] and B C = C_PsP

Here's the really neat part. We consider that our portfolio is made up of:

• Stock (with Price = P and dP = r P dt + s P dx)
• Call options on that stock (with value = C and dC = A C dt + B C dx)
• Money invested in a risk-free asset with constant return R (value = Q and dQ/dt = R Q)
• Then our Portfolio = n_s P + n_o C + Q
  here n_s and n_o are the number of units of stock and options
  and the fractions of our portfolio devoted to each asset are clearly
  u = (n_sP)/Portfolio, v = (n_oC)/Portfolio and w = 1 - u - v = Q/Portfolio

Now, both P and C are Ito processes ... so it gets interesting.
>zzz

• d(Portfolio) = n_s dP + n_o dC + dQ
        = n_s[r P dt + s P dx] + n_o[A C dt + B C dx ] + R Q dt
  where our risk-free asset grows at a constant rate R ... so dQ = R Q dt
• Rearranging somewhat:
  d(Portfolio) = [r dt + s dx ] n_sP + [A dt + B dx] n_oC +[R dt] Q
• Since the fractions of our Portfolio devoted to each asset are u, v and w = 1 - u - v (as above), we can write
  the return on our Portfolio as:
• d(Portfolio) / Portfolio = [r dt + s dx ] u + [A dt + B dx] v +[R dt] w
  or, equivalently
• d(Portfolio) / Portfolio = [su + Bv] dx + [ru + Av + Rw] dt

See? It's [something]dx + [something]dt. Another Ito process!! That stochastic term, dx, is unfortunate, but now comes the really neat part. We design our Portfolio to be risk-free. That is, we choose the fractions of our Portfolio devoted to stock and options, u and v, so that [su + Bv] = 0 thereby eliminating the random component introduced by dx. In other words, we want the Variance of our Portfolio to be zero and it's that $@#!* stochastic component that generates Variance and Volatility... what some people call "risk" (for no good reason which I can figure):

        Var[d(Portfolio) / Portfolio] = Var[(su + Bv) dx] = 0.

That means we Expect our riskless Portfolio to grow at the risk-free rate, R.

• We have: d(Portfolio) / Portfolio = [r dt + s dx ] u + [A dt + B dx] v +[R dt] w
  and, setting su + Bv = 0 (so the dx terms goes away), we put the Expected Portfolio growth rate = R:
• E[d(Portfolio) / Portfolio] = [r dt ] u + [A dt] v +[R dt] w = [ru + Av + Rw] dt = R dt
  meaning it grows at the risk-free rate R.

We now have the Black-Scholes-Merton equations:

1. su + Bv = 0   so that that u/v = - B/s
2. [ru + Av + Rw] = R   so that ru + Av + R(1-u-v) = R   so that u/v = -(A-R)/(r-R)

Equating u/v, from 1 and 2, we get:
        B/s = (A-R)/(r-R)   or

(r-R)/s = (A-R)/B

This says that the Sharpe Ratio, namely (Return - Risk-Free)/StandardDeviation, must be the same for the stock as for the option.
>Huh? How do you do that? Search for stocks that ...?
No, we can do nothing about the stock parameters. What we're talking about is finding the "appropriate" price for the option. Black-Scholes is saying that this "appropriate" price is when the Sharpe Ratio for the option is the same as for the stock. It gives us a necessary relation between the option parameters ... as we'll see in 3, below.

Now, collecting various results we have so far:

1. dC = C_t dt + C_P dP + (1/2) C_PP s²P²dt = [C_PrP + C_t + (1/2)C_PPs²P²]dt + C_PsPdx = AC dt + BC dx
   and
2. (r-R)/s = (A-R)/B     so A = R + B(r-R)/s
   which gives
3. AC = RC + BC(r-R)/S
   and, using the definitions of AC and BC given in [!!],
   this is a partial differential equation for the value of the Call Option, namely:
4. C_t + R P C_P+ (1/2)s²P² C_PP = R C

>Don't you find this confusing?
Yes ...

We now have the Black-Scholes partial differential equation, where we must attempt to solve for F(t,P) where P(t,x) is a Geometric Brownian Process and x(t) is a Brownian Motion.

>Mamma mia! Can't we simplify the notation?
Yes. Let's forget everything we've said so far.
Let's just consider a function F(t,y) which satisfies a certain partial differential equation.

[Black-Scholes] The Black-Scholes partial differential equation for F(t,y) is: Ft + R y Fy+ (1/2)s2y2 Fyy = R F with y a Geometric Brownian Process satisfying dy = (r dt + s dx)y, x(t) being a Brownian Motion.

>That's simpler? You just replaced P by y.
Yes.
Notice that the variable y(t) satisfies dy/y = r dt + s dx where, for our stock, r is the Mean return and s the Volatility.

>I assume we're going to solve that?
You mean [Black-Scholes]? Maybe ...

We have the stock Price, from [Ito*], above:
[1]             P(t) = P(t₀) exp[(r-s²/2)(t-t₀) + s (x(t)-x(t₀))]
Hence, taking logs:
[2]             log[P(t)] = log[P(t₀)] + (r-s²/2)(t-t₀) + s (x(t)-x(t₀))
The differential is then:
[3]            d(log[P(t)]) = (r-s²/2)dt + s dx(t)

Now x(t) is a Brownian Motion with random Brownian steps.
After a time t - t₀, the deviation from its initial position, X(t) = x(t) - x(t₀), is Normally distributed with Mean = 0 and Standard Deviation = SQRT(t - t₀). We'll denote this by: X(t) = N[Mean,SD] = N[0,SQRT(t - t₀)]
>That ol' square-root-of-time thingy, eh?
Yes. And that "s" out in front of dx(t) provides extra volatility so ...
>Huh?
If X has a certain Mean and Standard Deviation, say Mean = M and SD = S,
then A + B*X will have Mean = M+A and SD = B*S.
In particular, if X = N[M,S], then A + B*X = N[M+A,B*S]

Now look at [2], above, which we can rewrite as:
    log[P(t)/P(t₀)] = (r-s²/2)(t - t₀) + s (x(t)-x(t₀))

It has the form log[P(t)/P(t₀)] = A + B*X(t) with
A = (r-s²/2)(t - t₀) and B = s and X(t) = x(t)-x(t₀).

We conclude that ...

>Wait! That A and B aren't the same as we had before, with dC = ACdt+BCdx, right?
Right. Keep awake.
Remember that X(t) has Mean = 0 and Standard Deviation = SQRT(t - t₀).

We conclude that log[P(t)/P(t₀)] = A + B*X(t) will have Mean = A and SD = B*SQRT(t - t₀).
[4]             log[P(t)/P(t₀)] = N[(r-s²/2)(t - t₀), s SQRT(t - t₀)]
>Hey! log(P) is normally distributed, that means that P itself ... it's ... uh ...
Yes, lognormally distributed.
>Is that for real?
Real? We're talking mathematical models of what's Real. We'd have to test it against historical prices to see how well it mimics the Real world. (See normal-lognormal distributions.)

>I see that standard deviation for P, it's s*SQRT(time) again.
In [4]? Yes, but it's the SD for log(P). It's saying that we should expect log(P(t)) to be Normally distributed with a Mean or Expected value of log[P(t₀)] + (r-s²/2)(t - t₀) and a Standard Deviation of s SQRT(t - t₀). Notice that the Expected value grows linearly with time and the SD grows as the square root of time.

Before we proceed to Option stuff, the P-distribution can be derived from the fact that log(P/Po) is Normal with Mean and Standard Deviation as given above:

[Lognormal] The (lognormal) distribution of Prices P at time T = t - t0 is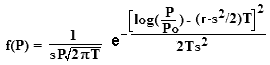

Okay, let's look at Expected Stock Price at time T, namely   P f(P) dP
We'll run through this quickly ...

To calculate the Expected Price we integrate, from P = 0 to P = infinity:
P f(P) dP = 1/{s SQRT(2πT)} e^{[-{log(P/Po)-(r-s2/2)T}2/{2Ts2}]} dP
    = A e^{-B{log(P) - C}2} dP   where A = 1/{s SQRT(2πT)} and B = 1/{2Ts²} and C = log(Po) + (r-s²/2)T.
>zzzZZZ
Wait! The result may surprise you. Just wait till the end, okay?
>zzzZZZ
Now put z = log(P) - C so P = e^z+C and dP = e^z+C dz and,
when P goes from 0 to infinity, z goes -infinity to infinity.
Hence the Expected Price is the integral, from z = -infinity to infinity of:
      A e^-Bz2 e^z+Cdz = A e^C+1/4Be^{-B(z - 1/2B)2}dz
Now put x = SQRT(2B)(z - 1/2B) so dx = SQRT(2B) dz ... and x also goes from -infinity to infinity.
Hence the Expected Price is the integral, from x = -infinity to infinity of:
            A/SQRT(2B) e^C+1/4B e^-x2/2dx
But 1/SQRT(2π) e^-x2/2 is the standard normal distribution (Mean=0, SD=1) and
Hence, substituting for A, B and C, we get the Expected Stock Price, at time T, as ... surprise!:

>Huh? The stock grows at the Mean Rate r?
No, the Expected price, E[P(T)], grows at the rate r (assuming continuous compounding at the annual rate r).
Of course, this continuous compounding gives a somewhat larger annual return than r itself, since e^r > 1+r.
However, the result shouldn't be surprising; we've gone full circle. Remember, we assumed (in [Ito]) that
dP/P = r dt + s dx from which it follows that, over the time interval dt, the expected rate of change is E[dP/P] = r dt

>Remember that equation [3]? It says ...
Yes, I remember. I'll repeat it here:
[3]            d(log[P(t)]) = (r-s²/2)dt + s dx(t)

>Well d(log(P)) = dP/P so it says dP/P = (r-s²/2)dt + s dx(t) so ...
I know exactly what you're going to say:
E[dP/P] = E[(r-s²/2)dt] + E[s dx(t)] = (r-s²/2)dt     since E[dx] = 0 for a Brownian Motion.
And that's different from E[dP/P] = r dt, right?

>You took the words right out of my mouth!
So you look at E[dP/P] = (r-s²/2)dt   or maybe   r dt and you're wondering which is correct, right?

>You took the words ...
But you forgot the magic rule for differentiating:

For P(t,x) where x is a Brownian Motion:                 dP = Pt dt + Px dx + (1/2)Pxx dx2                 and dx2 = dt

See that funny, extra term (1/2)P_xx dx²?
It can also be written (1/2)P_xx dt.

For our stock Price: P = Po exp[(r-s²/2)(t-t₀) + s (x(t)-x(t₀))]
      P_t = (r-s²/2) P dt
      P_x = s P dx
      P_xx = s² dx² P = s² P dt
      so dP/P = (r-s²/2) dt + s dx + (1/2)s² dt = r dt + s dx
      so E[dP/P] = r dt
      and that funny, extra term cancels the s²/2 leaving us with just r !

>How am I going to remember all those Ito rules? Why don't you ...?
Good idea. A summary is here: a dozen steps from Ito to Black-Scholes.

However, concerning the difference between r-s²/2 and just plain ol' r:

• If some random variable, say Y, has a lognormal distribution that means that log(Y) has a normal distribution
• To put it differently, Y = e^X is lognormal if X is normal
• Since X is normally distributed, 50% of the Xs lie above the Mean of the X variables: E[X]
• Since Y = e^X then half of the Ys lies above e^E[X]
• The Y-value for which half are above, half below ... that's called the Median of the Ys
• In [4], we note that log(P(t)) is lognormal (since its logarithm is normal)
• Indeed, the Mean of log[P(t)] over a time length T (namely t-t₀) is (r-s²/2)T
• We conclude that the Median of stock prices (at time T) is e^(r-s2/2)T
• If T is measured in years, then e^(r-s2/2) is the Gain Factor per year (in order to achieve the Median price)
• That corresponds to an Annualized Return of r-s²/2 (sometimes called the Median return)

>That looks familiar.
Yes. If the Mean return is r, then the annualized return, for a lognormal distribution of returns, is r-s²/2.

You can also play with this online spreadsheet which shows the difference between the Mean and the Median (for your choice of T):   CLICK!
Remember: Half of the prices are above and half below Po e^(r-s2/2)T

Okay, on to Option pricing:
If our option with strike price K, expires a time T in the future (so T is our t - t₀), then it's worth $(P- K) if P>K or $0 otherwise. Hence, at time T, it's worth Max(P-K,0).

We need to determine the expected value of this, namely E[Max(P-K,0)]
To find out what it's worth today we discount this at some risk-free rate, R.

[5]             Option Price = C = exp(- RT)E[Max(P-K,0)]

>What!? I thought R was the average stock return.
No, that's r.

In fact, this discounting at a risk-free rate is to incorporate the so-called principle of Risk Neutral Evaluation. The factor exp(- RT) does this. Although one might expect to use (1+R)^-T to provide the discounting, one normally (for the convenience of math-types) assumes continous compounding so, for N time periods within the time T, and interest R/N (in each period) we'd have (1+R/N)^-NT = [(1+R/N)^N]^-T which, as N infinity, has a limiting value of [e^R]^-T = e^{- RT}.

Further, we've already said that for our riskless Portfolio we'd expect it to grow at the risk-free rate ... which we're calling R. The interesting thing is that r, the Expected growth rate of our stock, no longer appears anywhere. That's because the Black-Scholes "riskless" Portfolio eliminates the stock return as a variable. It assumes the investor is "Risk Neutral" (as opposed to "Risk Averse").
>It ignores the stock return?
Yes. When I first saw Black-Scholes I thought this was really weird. Now I understand it ... sorta. In addition to eliminating r, Black-Scholes also ignores transaction costs and dividends and taxes etc. ... but other analysts have incorporated such variables.

Anyway, forging ahead ...
Suppose f(x) is the distribution density for some variable x which is nonzero on (0,infinity).
Then the average or Expected value of a function of x, say w(x), is: E[w] = w(x) f(x) dx
Since Max(P-K,0) is nonzero for P on (K,infinity) we have
[6]       C = exp(-RT)E[Max(P-K,0)] = exp(-RT)(P-K) f(P) dP = exp(- RT)Pf(P)dP - exp(-RT)K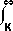f(P)dP
where f(P) is the distribution of prices, namely a lognormal distribution with certain Mean and Standard Deviation.
(The Normal distribution density with Mean = m and SD = S is given in Normal, above.)

For our Prices, the distribution of log[f(P)] is normal and the distribution of P is ...

>Given in equation [-1], eh? By the way, isn't -1 an odd number?
[-1] an odd number? Well, it certainly isn't an even number.

Anyway, substituting our expression for P(t), from [4], into [6], and using the distribution shown in [-1] and executing some hand-waving we get (using a somewhat different notation than given in Options):

>What!? That's a LOT of hand-waving!
Uh ... yes, but you can pick out the square-root-of-time, and the Normal "standard" distribution stuff
("standard", meaning Mean=0 and SD=1) and the Standard Deviation of stock returns and
K*N(d₂) is the (strike price)*(probability that the stock price will be above K) ... so the option is exercised ... and
e^RTP(0) N(d₁) would be the Expected value of a variable which equals P if P>K and 0 otherwise ...
and e^RTP(0) N(d₁) - K*N(d₂) is the Expected option value at maturity ... and multiplying this by e^-RT gives what should be the current option value, using that risk-neutral valuation.

>That's still a LOT of hand-waving!
Yes, but just remember that, since f(P) is a probability density defined for P>0, then, from

[6]       C = exp(- RT)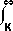Pf(P)dP - exp(-RT)K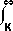f(P)dP

1. f(P)dP is the probability that the stock Price lies in (P,P+dP)
2. the integral of f(P)dP from 0 to infinity is the probability that Price > 0, namely 1 (meaning certainty)
3. the integral of f(P)dP from K to infinity is the probability that Price > K
4. the integral of Pf(P)dP from K to infinity is the Expected or average value of Prices > K
5. then 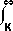Pf(P)dP - K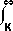f(P)dP = (Average of those Prices greater than K) -K(probability that Price > K)

I'm camping as I write this, the sky is blue, sun is shining and I'm without Net access, and I need to do more thinking ... between fishing, playing with the grandkids and roasting marshmallows

If the volatility of notation, randomness of thought and unpredictable continuations are getting you down
... check out the summary