We consider, at some point in time, the various monthly gains in our portfolio over the past N months ... like so (where the number of occurrences of each gain, out of N = 200, is plotted): The spread about the average (or mean) gain is measured by the Standard Deviation: SD2 = (1/N)Σ (Gk - A)2 where there are N portfolio gains, Gk (k=1 to N), and A = (1/N)ΣGk is their Average (or Mean) and SD is the Root Mean Square Deviation between the gains and their average and it can also be computed like so: SD2 = (1/N)Σ Gk2 - {(1/N)ΣGk}2

Fig. 1 A 10% monthly gain is unusual, but what the heck. It looks like a Normal Distribution, but that's an accident!

To prove this we first drop the subscripts (for sanitary reasons) and write:
SD² = (1/N)Σ (G - A)² = (1/N)Σ{G² - 2GA + A²} = (1/N)ΣG² - 2A(1/N)ΣG + (1/N)ΣA²
    = (1/N)ΣG² - 2AA + (1/N)NA² = (1/N)ΣG² - A²

Mean = 10.1%
Standard Deviation = 15.8%
Maximum Deviation magnitude = 39.8%     in 1952
Average Deviation magnitude = 13.1%

Fig. 2 & 3 Distribution of 200 Normally Distributed monthly returns where each has doubled

Now, suppose the individual gains are changed by ADDING a constant C (rather than multiplying by a constant λ) Here's a picture of two stocks whose returns differ by a constant We have, as the new average: (1/N)Σ(G + C) = (1/N)ΣG + (1/N)ΣC = (1/N)ΣG + (1/N)NC     = A + C hence the new Standard Deviation: (1/N)Σ{(G + C) - (A+C)}2 = (1/N)Σ{G - A}2 = SD2 In other words, the SD is unchanged by the addition of a constant. (Uh ... did I mention that we dropped the subscripts again?)

One important consequence of these results is that if we have a collection of numbers, say {G_k},
with Mean = 0 and SD = 1, then the collection {λ G_k + C} will have Mean = C and Standard Deviation = λ.

Write:

     Increases in those gains which are LESS than the average gain, will cause the SD to decrease.
     Decreases in those gains which are GREATER than the average gain, will also cause the SD to decrease.

That's sort of obvious since SD measures the spread of gains about the average. Increasing the smaller gains and/or decreasing the larger gains will reduce this spread, hence the SD. Indeed, for a Normal Distribution (the infamous "Bell Curve"), about 2/3 of the returns lie between Mean - SD and Mean + SD. Stare at the above graphs and convince yourself that this is true. (For the first graph, this range is from 10% - 20% = - 10% to 10% + 20% = 30%.) When SD decreases, these 2/3 crowd closer to the Mean.

Now suppose MY monthly gains are all increased by some positive constant C compared to YOUR monthly gains.(Say C = 30%, that'd be nice.) As we've seen, SD, hence the volatility, doesn't change. Our graph just gets shifted to the right by an amount C. Same spread, same SD, same volatility. But wouldn't you say that the risk has decreased, for my portfolio? After all, my gains are now 30% higher than yours. Less risky, right? Alas, the investment community says the risk is the same for both our portolios because they normally DEFINE risk as the Standard Deviation (and not as the risk of a loss). For this association of "risk" with "SD", see 1 and 2 and 3 and ... and n. Even William Sharpe defines the Return per unit of Risk as some Return divided by the Standard Deviation!

Fig. 4

Now suppose MY monthly gains are all increased by some positive multiplier F > 1 compared to YOUR monthly gains. If your monthly gains are all positive, then F = 2 would be nice. That'd make my gains twice the size of yours. As we've seen, SD, hence the volatility, changes by the same factor. All the gains in MY distribution graph get shifted to the right by a factor F, the spread increases by that factor and the SD (and the volatility) change by the same factor. (The height of my graph decreases 'cause the number of returns hasn't changed, so there are fewer in each of the intervals along the horizontal axis - because of the increased spread.) Because of this increased spread, there is a greater probability of Returns far from the mean; that's the extended tail of the distribution chart. For some distributions, this extended tail means a greater chance of disastrous Returns! (See Kurtosis) See Fig. 3, compared to Fig. 2, or, better still, here's a closeup of the tails: Fig. 5a The tail of the distribution

Fig. 5

But, if all YOUR gains were positive, wouldn't you say that the risk has decreased, for my portfolio? After all, my monthly gains are now higher than yours by the factor F. Less risky, right? Alas, the investment community says the risk is higher for my portfolio because (have we said this before?) they usually DEFINE risk as the Standard Deviation ... and that's increased!

Fig. 6

One other thing: the charts above look like Normal Distributions. Well ...uh, they are, but it's only so I could get pretty pictures. The real, live monthly returns for, say, the S&P 500 look sorta Normal ... but that's not important for what we're discussing.

Fig. 7

Oh yeah ... one other thing: We often (?) hear that the Standard Deviation increases as the time interval increases. In fact, a common statement is that SD varies as the square root of the time: SQRT(time). This follows (mathematically speaking) from Einstein's 1905 analysis of a random walk (or Brownian Motion) and, earlier, it's associated with Louis Bachelier and even earlier with Jules Regnault (See this.PDF). It assumes the returns are random in this sense. Are they? Looking at all intervals of length 1 month, 6 months, 12 months, etc., and calculating the SD for each set, we get this chart. Close, but no cigar.

P.S. The argument goes something like this:

If you start at x = 0 and take N steps of length x₁, x₂, ...., x_N then your distance from the origin (x = 0) is R where, to get the Standard Deviation of the set of distances from the origin (over all possible sets x₁, x₂, ... ), we consider the Mean Square of R ... hence we consider:
R² = (x₁+ x₂+...+ x_N )² = x₁²+ x₂²+... +x_N² +2x₁ x₂ +2x₁ x₃+ ...
If the Mean = 0 (for the steps x₁, etc.), then each is equally likely to be positive as negative and, for large N, the cross terms like x₁x₂ will average to zero and we're left with
R² = x₁²+ x₂²+... +x_N² = N { (x₁²+ x₂²+... +x_N²)/N } = N {Standard Deviation of the x's}²

leaving us with: R = N^1/2 {Standard Deviation of x's} ^* ... and the square root pops up.
If the number of steps, N, increases with time, then this is proportional to SQRT(time).

See also Square Root of Time

In general, if SD(N) and SD(M) are the Standard Deviations of N- and M-month returns, we can write:

To annualize "Monthly" returns, we can do the following:

• Calculate the Standard deviation of Monthly percentage Returns (over, say, 36 months).
• Annualize this SD of 1-month returns by writing:

Hence, the Standard Deviation of annual returns (meaning 12-month returns) will should may be estimated as

so y'all just multiply the Standard Deviation of monthly returns by the square root of 12 in order to estimate the Standard Deviation of annual returns.

If we wanted the SD of annual returns and observed these annual returns over a 36 month period, we recognize that there would only be three returns to consider (in this 3-year period)! So we can take the SD value for monthly returns (there's 36 of them!) and multiply by SQRT(12) = 3.46 (roughly) to get estimate the SD of 1-year returns.

>That's assuming you believe in this Square-Root-of-Time stuff.
Right! But it makes some sense. After all, one would expect the 12-month gains to be 12 times the monthly gains (roughly), so the Mean Squared Deviation would be 12² times larger, but over any given time interval (like N years worth of gains), there would be 1/12 as many terms in the sum (1/N)Σ (G_k - A)² so we're up by a factor 12²/12 = 12 and the Standard Deviation (being the square root of the Mean Squared Deviation) would be SQRT(12) times larger ... roughly.

>I haven't the foggiest idea what you just said.
Here's an example. Over the 51-year period Dec/50 to Dec/00 the 1-year returns for the S&P 500 averaged 10.1% - that's the return for the year ending Dec 31/50, then the return for the year ending Dec 31/51, etc..

The Standard Deviation of these fifty-one annual returns is was 15.8%. On the other hand, the Average monthly return was 0.79% and the Standard Deviation of these monthly returns was 4.09% (and there were 12 x 51 = 612 of these monthly returns). The ratio of SD(Annual)/SD(Monthly) = 15.8/4.09 = 3.86 whereas SQRT(12) is ... uh ... >3.46 (roughly)? Right! >And I notice that the 12-month average return is larger than the average 1-month return by a factor 10.1/0.79 which is ... uh ... 12, roughly.

>12.78, actually.
However, I should mention the following:

• We consider just monthly returns over N months.
• We calculate the Standard Deviations of these monthly returns, as N increases.
• We get an decreasing Standard Deviation!!

>Didn't you just say the Standard Deviation increases?
That's if you consider the Standard Deviation on N-month returns. What I'm talking about now is the Standard Deviation of 1-month returns, over N months. See the difference?

>No!
Then just look at this picture. See? The variability decreases as N, the number of 1-month returns, increases.

---

Okay, if the risk (in the investment guru sense, meaning Standard Deviation) goes UP when the time period increases, what about the risk (in the dictionary sense)?

risk n. The possibility of suffering harm or loss. -v To expose to the possibility of harm or loss.              (That's not my definition of risk. It's Webster's.)

We want to investigate the possibility of suffering harm or loss, so here's what we'll do (for investing in the S&P 500, for example):

We look at all 1-month intervals between Jan 1, 1970 and Jan 1, 2000 (that's thirty years and 360 such 1-month intervals) and count the number of times we would have LOST money. Then we look at all 6-month intervals, then 12-month intervals, ... then 120 month-intervals. (The last is 10 years, right? And there's 240 120-month intervals between Jan 1/70 and Jan 1/00.) For each we plot the percentage of intervals when we would have lost money (i.e. the gain over the given N-month period was less than 1). (That's our suffering harm or loss.)

We'd get: Fig. 8 risk HAS decreased with length of investment horizon! ... and, for the NEXT thirty years?

Fig. 9 Showing the average of the N-month gains, annualized. P.S. Note that the '87 CRASH is just a minor blip!

Of course, in addition to the risk of loss, we should consider the degree of risk ... maybe like so:

Fig. 10 The percentage of times that we would have incurred a Loss of P% (Jan 1,1970 to Jan 1, 2000)

For example, in all the 3-year intervals (between Jan/70 and Jan/00), 4% of them would have suffered a loss of at least 20%.

'course, mebbe the time length (30 years) is too short (too small a sample?), so here's 50 years:

Fig. 11 The percentage of times that we would have incurred a Loss of P% (Jan 1,1950 to Jan 1, 2000)

---

and then there's: Fig. 12 ... but, what about the NEXT thirty years?

Fig. 13

---

and: Fig. 14

Fig. 15

---

and finally: Fig. 16

Fig. 17

Fig. 18 There were 64 10-year periods in Oct/84 - Jan/00. None suffered a loss of 5% or more. Data obtained

Uh ... one more thing. The set of monthly gains for, say the S&P 500, may be rearranged and the rearranged set will have identical Distribution, Mean and Standard Deviation. For example, if we were to rearrange the gains so they occur from Minimum to Maximum (over the past thirty years) the S&P would look quite different (though it'd end up at the same place). If the ordering were from Maximum to Minimum ... well, a picture is worth a $1000 words:

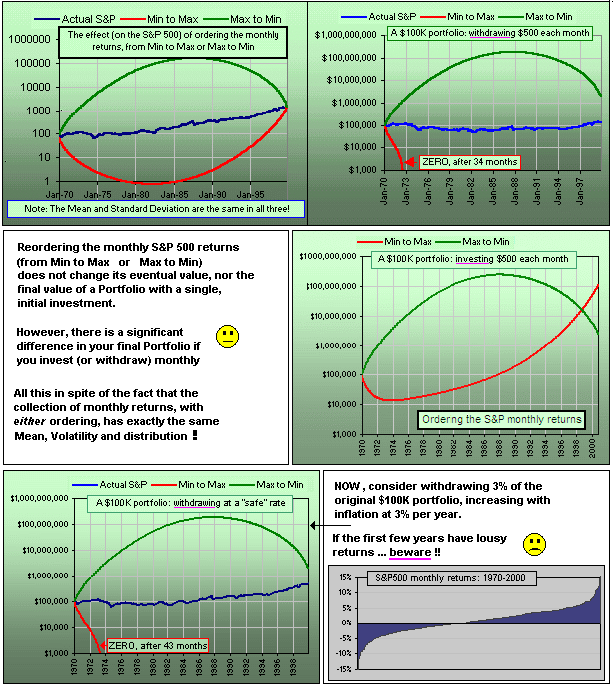
Fig. 19 The best of times, the worst of times ...

And if we invest in the S&P 500, but make monthly withdrawals? What'd our portfolio look like in each reordered case?
A BIG difference in the final result, eh what? (... yet the Distribution of Returns is the same.)

Or is it? If I invested in a stock that decreased by a fixed amount each month^*, there would be no uncertainty (SD = 0) and ... uh, no risk ... even tho' I lose every single month! No risk, eh?

Strange world, this world of investing. They've got a language of their own.

^* An investment with a constant negative return? Yeah, that's my mutual fund. You might like to invest in it.
I invest in GICs at 2% and my MER (Management Expense Ratio) is 3%