Every time I do some calculations I come up with that #$%@!*? Magic Sum, and it involves the reciprocal of some variable.

>Huh?
The reciprocals might be the reciprocal of stock prices or stock gains or portfolio values or ...

>Example?
Okay, for example, *** involves withdrawal rates which have the form W/P where W is the withdrawal amount and P is the portfolio. Assuming that W is a constant and that we know the distribution of the Ps, what's the distribution of withdrawal rates?

>The distribution of portfolios? What does that mean?
Don't you remember? We were following 10,000 investors, all of whom invest in some asset with a prescribed return distribution. (For example, a lognormal distribution with Mean Return = 9% and Volatility = 15%.)

Okay, let's concentrate on lognormal distributions.
We start with a variable, r, with a normal distribution described by f(r). This variable has Mean = M, SD = S.
We note this fact by writing: r = N[M,S] meaning r is Normally distributed with Mean = M, Standard Deviation = S.
Note: The "standard" notation is N[Mean,Variance], but here we'll use N[Mean,SD].

>M is the average annual return?
Well ... uh, actually, it's some return: average, annualized, whatever. The important thing here is that it's some constant. In practice I guess one would use annualized.

Okay, now we consider the variable: g = e^r which is then lognormal (by definition of "lognormal").

Suppose r represents annual returns, so that g represents annual gain factors.
Note that g = e^r is approximately 1+r, as expected. We can also consider that the return is continuously compounded where we divide the year into B seconds with a return of r/B per second so the "annual" return would be (1+r/B)^B which, for B = a few jillion, is indistinguishable from e^r.    

Over n years, the cumulative gain factor is the product of the annual factors, namely: g₁g₂...g_n = e^{r₁+r₂+...+r_n}

Now we consider reciprocal: 1/g = e^-r where the variable -r has Mean = -M, SD = S.
Over n years, the product of these reciprocals is 1/{g₁g₂...g_n} = e^{-{r₁+r₂+...+r_n}}

We now consider the Magic Sum: gMS(n) = I₁/g₁ + I₁I₂/g₁g₂ + I₁I₂I₃/g₁g₂g₃ + ... + I₁I₂...I_n/g₁g₂...g_n
where I₁, I₂, ... are annual inflation factors (an inflation rate of 3% means an inflation factor of I = 1.03)
and g₁, g₂, ... are the annual gain factors.

For the situation we're considering, the inflation rate is a constant, so I_k = I^k where I = 1+InflationRate = 1+i.
That gives: gMS(n) = I/g₁ + I²/g₁g₂ + I³/g₁g₂g₃ + ... +Iⁿ/g₁g₂...g_n

Here's our question: Given the g-distribution, what's the distribution of:   I/g₁+I²/g₁g₂+ I³/g₁g₂g₃+ ... +Iⁿ/g₁g₂...g_n ?

>So what good is this gMS?
In order that our portfolio last n years, the (initial) withdrawal rate must be less than 1/gMS.
In fact, if it were exactly 1/gMS then it would last exactly n years. This we call the Maximum Rate of Withdrawal

>We?
Well, I do. For example, the value of MRW for n = 30 years looks like this, for a S&P 500 portfolio.

>Do you see that notorious 4% "safe" withdrawal?
Yes, but we're talking S&P 500. Here's a picture for another allocation:

Both assume the sequence of annual returns occurs in historical order. Suppose they didn't. Suppose you started your retirement after a few bangup years on the market, like 1995-2000 when the S&P 500 skyrocketed. Suppose you started your retirement in, say, the year 2000. Your portfolio has ballooned. You expect to withdraw a percentage of this fat portfolio. As you might expect, the market tanked for the next three years! Indeed, if we took those 3 BAD years and stuck them in as the first 3 years of historical data, we' d get

Anyway, our goal is to establish the distribution of gMS(n).

To put it differently:

Starting with a $1.00 portfolio and an initial withdrawal rate of w, the value of our portfolio after n withdrawals is g1g2...gn[ 1 - w*gMS(n)]

Note that the guy out front, that's g₁g₂...g_n, is just the buy-and-hold portfolio, after n years.
We could, for example, assume that it's:

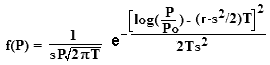
where Po = $1.00 and T = n, the number of years, and r and s are the Mean Annual Return and Standard Deviation (respectively).

>Huh?
It's noted here (as number 6).

Continuing, for our lognormal g-distribution, 1/g_k = e^-r_k so our Magic Sum becomes:

gMS(n) = I e^-r₁ + I² e^-(r₁+r₂) + I³ e^{-(r₁+r₂+r₃)} + ... +Iⁿe^{-(r₁+r₂+r₃...+r_n)}

Look at a particular term:
Iⁿe^{-(r₁+r₂+r₃...+r_n)} = e^{n log(I) -(r₁+r₂+r₃...+r_n)} = [e^{log(I) -(1/n)(r₁+r₂+r₃...+r_n)}]ⁿ

Our question now becomes: Given the r-distribution, what's the distribution of log(I) - (1/n)(r₁+r₂+r₃...+r_n) ?

As it turns out, if the annual returns r_k are independent and selected from the same normal distribution, (which is the case we're considering),
then log(I) - (1/n)(r₁+r₂+r₃...+r_n) is Normal with Mean = log(I) - M and SD = S.
That is: N[log(I) - M,S].

Okay, so we consider a variable z = e^q, where q is N[log(I) - M,S].
Since q is Normal, then z is lognormal and we then have:

gMS(n) = z₁ + z₁z₂ + z₁z₂z₃ + ... +z₁z₂z₃...z_n = e^q₁ + e^q₁+q₂ + ... + e^{q₁+q₂+...+q_n}

Note that, if we know the Mean and Standard Deviation of q (normally distributed), then we also know the Mean and Standard Deviation of lognormally distributed z = e^q (as noted here), namely:

A Mean(z) = eMean(q)+SD2(q)/2 = I e-(M-S2/2) = M SD2(z) = e2Mean(q)+SD2(q) [eSD2(q)-1] = I2e-2(M-S2/2)[eS2-1] = M2 [eSD2(q)-1] = S2

since Mean(q) = log(I) - M and SD(q) = S.

Our question now becomes:

If the set zk is lognormally distributed, what's the distribution of z1 + z1z2 + z1z2z3 + ... +z1z2z3...zn ?

>Don't you find that confusing? I mean ...? Let's just look at two years worth, so we consider just z1 + z1z2. Understand that, although z1 and z2 are selected from the same lognormal distribution, they are independent. Let's call them u and v. We pick a jillion values for u and plot their distribution. We then pick another jillion values for v, multiply by u, then plot the distribution of uv. Finally we plot the distribution of the jillion sums, like so

>So what's the distribution of ... uh ...?
Of z₁ + z₁z₂ + z₁z₂z₃ + ... +z₁z₂z₃...z_n ?
I have no idea ... but I'm thinking ...

We'll find the Expected (or Average) value of x*y where Mean(x), Mean(y) and SD(x), SD(y) are the Means of Standard Deviations of the two random variables x and y.

As noted here :
        { Mean(xy) - Mean(x) Mean(y) } = SD(x)SD(y) PC
where PC is the pearson correlation.

Since we're assuming that our variables are independent, then PC = 0 so that Mean(xy) = Mean(x) Mean(y)
... and that extends to a product with umpteen terms. That is, the Mean of a Product is the Product of the Means.

In particular, for our variables z₁, z₂, etc. (all of which are selected from the same distribution), we have:
Mean(z₁z₂... z_k) = Mean(z₁)Mean(z₂)...Mean(z_k) = Mean(z)^k
so, from A:
[1] ...         Mean(z₁z₂... z_k) = I^k e^-k(M-S2/2) = M^k
where M = I e^-(M-S2/2)

So we have:

B Mean(gMS(n)) = Mean(z1 + z1z2 + z1z2z3 + ... +z1z2z3...zn) = M + M2 + M3 + ... + Mn

>Do you know what you're doing?
That's questionable. Anyway, let's forge ahead.
For independent random variables x and y, we have a magic formula:
        SD²(x*y) = Mean²(x)SD²(y) + Mean²(y)SD²(x) + SD²(x)SD²(y)

Let's look at the relative size of these terms, for
M = 0.09 (that's a 9% return) and S = 0.15 (that's a 15% SD) and I = 1.03 (that's an inflation rate of i = 3%) and
Mean(x) = M = I e^-(M-S2/2) = 0.9520
SD²(x) = S² = I²e^-2(M-S2/2)[e^S2-1] = 0.0206
Then SD²(x*y) = (0.9520)²(0.0206) + (0.9520)²(0.0206) + (0.0206)(0.0206) = 0.0187+0.0187+0.0004

Since Mean²(z_k) = M² and SD²(z_k) = S² we can rewrite this as:
[3] ...         SD²(z₁z₂...z_k-1z_k) = Mean²(z₁z₂...z_k-1) S² + SD²(z₁z₂...z_k-1) (M² + S²)

We'll go step-by-step:

Product		Mean2	SD2
z1		M2	S2
z1z2		M4	(M2+S2)2 - M4
z1z2z3		M6	(M2+S2)3 - M6
...		...	...
z1z2z3...zk		M2k	(M2+S2)k - M2k

We now have:

C SD2(gMS(n)) = SD2(z1 + z1z2 + z1z2z3 + ... +z1z2z3...zn) = Σ (M2+S2)k - ΣM2k

>Is that legal?
Yes. The Variance of a Sum is the Sum of the Variances ... provided the variables have zero correlation.

>There's that independence again, eh?
Yes. A simplifying assumption.

>Don't you feel uncomfortable with all those simplifying assumptions?
The proof is in the pudding ... as they say.

>So you think that z₁, z₁z₂, z₁z₂z₃ ... you think they're independent?
Well, not really. I think that assuming z₁, z₂, z₃ are independent, that's good. But z₁, z₁z₂, z₁z₂z₃? Not so good.

>So?
We'll start off with this simplifying assumption because ... uh, the proof is in the pudding. If we don't like what we get, we'll change it

For large values of n, formulas B and C reduce to:

Mean(gMS) = M / (1 - M)   as ninfinity
SD²(gMS) = (M²+S²) / [1-(M²+S²)] - M²/(1-M²)   as ninfinity

Remember our earlier example? M = 0.9520 and S² = 0.0206

That'd give:

Mean(gMS) = 19.8   as ninfinity
SD²(gMS) = 3.012   so   SD(gMS) = 1.734   as ninfinity

>So, what does all that mean?
Remember? The Maximum Rate of Withdrawal is 1/gMS(n).
The Expected value of gMS (for large n) is 19.8 and 1/19.8 = 0.051 or 5.1%

>For this particular example.
Yes, of course.

For smaller n-values, the Expected Value of gMS(n) is given by:     Mean(gMS(n)) = M (1 - Mn) / (1 - M) and 1/(Expected Value) is (1/M - 1) / (1 - Mn) which, for M = 0.9520 is shown here

>Uh ... I've forgotten. What's that M again?.
Okay, we'll look at A and B and sum the series and write:

D If portfolio returns are lognormally distributed with Mean and Standard Deviation M and S, and g1, g2, g3 ... are annual gain factors and I = 1 + i = 1 + InflationRate is the annual inflation factor and M = I e-(M - S2/2) and S2 = I2e-2(M-S2/2)[eS2-1] = M2[eS2-1] and gMS(n) = I/g1 + I2/g1g2 + I3/g1g2g3 + ... + In/g1g2...gn then Mean(gMS(n)) = M (1 - Mn) / (1 - M) SD2(gMS(n)) = (M2+S2) [1-(M2+S2)n] / [1-(M2+S2)] - M2 (1-M2n)/(1-M2) and 1/Mean(gMS(n)), namely (1/M - 1) / (1 - Mn), is and gives an estimate of the Maximum Rate of Withdrawal.

Note: A random selection of returns would give a variety of values for 1/gMS(n).
Perhaps what we need is not the reciprocal of the average of gMS(n) but the average of the 1/gMS(n) values.
That means we should look at the average of the reciprocals, not the reciprocal of the average, eh?
However, the reciprocal of the average is the smaller of these two numbers, so it's "safer" when we're estimating a rate of withdrawal.

>The proof is in the pudding, you said. So, is it any good?
I have no idea, but it sure avoids a jillion Monte Carlo simulations, eh?

However, look at this:

See? For an S&P500 portfolio, starting in 1928, gMS(n) 20 roughly

>I'd say that, so far, the only useful thing is that funny formula ... which is a complete mystery to me.
Okay.

• We start with the annual Gain Factors, each year: g₁, g₂, g₃, ...
  (That means that if $1.00 grows to $1.23 in a given year, then 1.23 is the Gain Factor for that year.)
• The annual Gain Factors are reduced by the Inflation Factor: I = 1+i to give g₁/I, g₂/I, g₃/I, ...
• The value of your portfolio, after n years, turns out to be:
  g₁g₂g₃...g_n [ 1 - w(I/g₁ + I²/g₁g₂ + I³/g₁g₂g₂ + ... + Iⁿ/g₁g₂g₂...g_n) ]
  where w is your initial withdrawal rate. (If it's 4.5% then w = 0.045)
  (The subtracted terms, like w I/g₁ and w I²/g₁g₂ are the loss of portfolio dollars ... due to your withdrawals)
• We conclude that the value of your portfolio, after n years, is the value of a buy-and-hold portfolio (without withdrawals), namely g₁g₂g₃...g_n, multiplied by 1 - w gMS(n)
  where gMS(n) = I/g₁ + I²/g₁g₂ + I³/g₁g₂g₂ + ... + Iⁿ/g₁g₂g₂...g_n
  (Note that the terms are all of the form of a product of   InflationFactor/GainFactor)
• Whether or not your portfolio will survive n years will depend upon whether 1 - w gMS(n) is positive or negative.
• For your portfolio to survive, you'll need 1 - w gMS(n) > 0 so you should withdraw less than 1/gMS(n).
• To this end, we consider 1/gMS(n) ... to be sure that w is less than this.
• The Expected Value of gMS(n) (as derived above ... with certain assumption!) is: M + M² + ... + Mⁿ
  where M is the Expected InflationFactor/GainFactor = I/(AnnualizedGainFactor)
• For a lognormal distribution of returns, Annualized Gain Factor = e^{M - S2/2}
  (In fact, M - S²/2 is an excellent approximation for annualized returns ... if you know the Mean and Standard Deviation!)
• Then M = I / e^{M - S2/2}.
• To deal with M + M² + ... + Mⁿ, we then need to evaluate a sum of the form:
  (1)     SUM = 1+x + x² + ... + x^N-1
  We multiply by x and get
  (2)     x SUM = x + x² + x³ + ... + x^N
  Subtract (2) from (1) and get:
  (3)     (1-x)SUM = 1 - x^N   so   SUM = (1 - x^N) / (1-x)
• We use this to evaluate our sum, which we write as: M[1 + M + M² + ... + M^n-1]
  This gives: Expected Value of gMS(n) = M [1 - Mⁿ] / [1 - M]
• Recall that we're interested in 1/gMS(n) so, inserting the Expected Value of gMS(n)
  and substituting M = I / e^{M - S2/2} and staring at the reciprocal of that Expected Value of gMS(n),
  namely [1 - M] / [1 - Mⁿ] / M = [1/M - 1] / [1 - Mⁿ] we get voila!
  ... the funny formula for our estimate of the Maximum Rate of Withdrawal:

  

>zzzZZZ You may be interested to know that, even if I believed the above stuff, I still have no idea what's the distribution of gMS values ... but if I generate a thousand gMS values (using random lognormal returns) and plot their distribution (as described here), it looks like this Doesn't it look familiar? That lognormal curve has the same Mean and Standard Deviation as the thousand-value sample. >zzzZZZ

How about a calculator, using that funny formula?

Mean Annual Return = % Standard Deviation = % Inflation Rate = % Number of Years = Maximum Rate of Withdrawal = % ... maybe :^)

>zzzZZZ

to continue