Okay, here's what we have, so far:

If portfolio returns are lognormally distributed with Mean and Standard Deviation M and S, and g1, g2, g3 ... are annual gain factors and I = 1 + i = 1 + InflationRate is the annual inflation factor and M = I e-(M - S2/2) and S2 = I2e-2(M-S2/2)[eS2-1] = M2[eS2-1] then your portfolio, after n years, is given by:   g1g2...gn[1 - WgMS(n)] where W is the (initial) withdrawal rate (increasing with inflation) and gMS(n) = I/g1 + I2/g1g2 + I3/g1g2g3 + ... + In/g1g2...gn In order that your portfolio survive n years, 1 - WgMS(n) > 0 or   gMS(n) < 1/W. Further we have (from Part I): Mean(gMS(n)) = M (1 - Mn) / (1 - M) SD2(gMS(n)) = (M2+S2) [1-(M2+S2)n] / [1-(M2+S2)] - M2 (1-M2n)/(1-M2)

>So, what're the chances that my portfolio will survive, say, 40 years? Okay, we saw in Part I that the distribution of gMS(n)-values looks rather lognormal ... like so >Huh? "Looks rather lognormal"? Are you kidding? I'm saying that we're going to assume that gMS(n) has a lognormal distribution. >Can you do that? Why not? Everybuddy assumes that the distribution of S&P500 returns or DOW returns or GE or MSFT returns or (almost) any stock returns are lognormal, eh? But look at the monthly S&P returns, from Jan/1950 to Jan/2002 Are they lognormal? >It's close. Right, and the gMS(n) distribution is close to lognormal. >Aah, but it also makes the math simpler, eh? Well ... uh, yes.

>Okay, let's see what you get.
Thank you.
We have the Mean and Standard Deviation of gMS(n), given above. We're calling them Mean(n) and SD(n).
Mean(n) = M (1 - Mⁿ) / (1 - M)
SD²(n) = (M²+S²) [1-(M²+S²)ⁿ] / [1-(M²+S²)] - M² (1-M²ⁿ)/(1-M²)

Then:

• If the gMS distribution is lognormal, the gMS(n)-values are equal to e^Z for some normally distributed variable Z.
• Further the Mean and SD of the Z-variable - we'll call them M(n) and SD(n) - are related to Mean(n) and SD(n).
• The relation (given here) is:
  SD²(n) = log[1+SD²(n) / Mean²(n)]
  M(n) = log[Mean(n)] - SD²(n)/2 = (1/2)log[Mean²(n)/{ 1+SD²(n) / Mean²(n) }]
• We are now in a position to generate the distribution of gMS(n)-values, for any n.

>The assumed distribution ... and you also need the mean and ... Yes, yes. We'll try it out for n = 40 years and: Mean Portfolio Return = M = 0.09 (or 9%) Standard Deviation of Portfolio Returns = SD =0.15 (or 15%) Inflation = 3% so I = 1+i = 1.03 Then M = 0.9520, S = 0.1436 and Mean = 17.06, SD = 1.610 and M = 2.832, SD = 0.0941 The resulting distributions (for a few n-values) is here where we plot eZ where Z has a normal distribution which, for n = 40, has mean = 2.832 and standard deviation = 0.0941.

Figure 1

>What does that tell you?
We're interested in the fraction of portfolios for which gMS(n) < 1/W.
If W = 0.05 (meaning a 5% withdrawal rate, initially), then we'd want gMS(n) < 1/0.05 or gMS(n) < 20.
Look at the 40-year graph. Some fraction of portfolios actually have gMS(n) < 20. See the dot?

>Looks like about 95%. Actually, it's 95.8%. >So 95.8% of portfolios are "safe"? Yes, with a 5% withdrawal rate. >It's hard to see. Can't you blow up that part? Yes. It's here where the fraction of surviving portfolios are shown for various values of n, the number of years of withdrawals >For 30 years I can withdraw 5% with over 98% probability of surviving, right? Right. The green dot.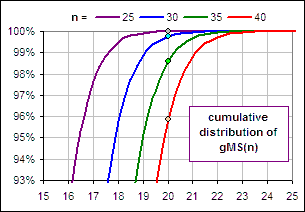

Figure 2

>Don't you have a formula for that probability of survival?
I'm still thinking.

>And do you believe all this stuff?
Don't ask.

Okay ... on to the probability of portfolio survival:

• The gMS-values (generated by randomly choosing portfolio returns from a lognormal distribution) are equal to e^Z.
• Surviving portfolios will have gMS < 1/W.
• In order that this inequality is satisfied we'll need e^Z < 1/W hence Z < log(1/W).
• But Z is Normally distributed with Mean and SD equal to M and SD.
• In other words, the Z-distribution is N[M,SD]
  where N[mean,sd] is our notation for a normal distribution with prescribed mean and sd.
• (A plot of a N[M,SD]-distribution will look like one of the graphs in Figure 1
  ... and the "standard" cumulative distribution, N[0,1], is shown below in Figure 3A)

  Figure 3A	Figure 3B

• Suppose that the function describing the cumulative probability for this "standard" distribution is N(x), where N(x) runs from 0 to 1 (meaning 0% to 100% probability).
  The function describing our distribution, N[M,SD], is then N((x-M )/SD)
  (meaning we shift the curve horizontally a distance M, to centre it at the mean, then stretch the horizontal scale by dividing by SD as in Figure 3B).
• We want to know the probability that Z < log(1/W),
  so we look at the value of N((x-M )/SD) when x = log(1/W).
• We conclude that the probability of survival, for n years with a withdrawal rate of W is N( (log(1/W)-M )/SD)
• In MS Excel, this means we evaluate NORMSDIST(( log(1/W)-M )/SD).

>Neat! So we just plug in the portfolio return and ...
No! We're a long way from the portfolio parameters. We have to go back and note that the M and SD that we use here depend upon Mean and SD, the Mean and Standard Deviation of gMS which, in turn, depend upon the Mean and Standard Deviation which we called M and S which in turn depend upon M and S, the portfolio parameters.

>Aha! Now I see why they're colour coded so that ...
Let's just do it, okay?

>Can you just give the final result?
Okay, here are the relationships:

1. M and S are the portfolio parameters: Mean and Standard Deviation.
2. M = I e^{-(M - S2/2)} and S² = I²e^-2(M-S2/2)[e^S2-1] = M²[e^S2-1]
3. For gMS we have:
   Mean(n) = M (1 - Mⁿ) / (1 - M)
   SD²(n) = (M²+S²) [1-(M²+S²)ⁿ] / [1-(M²+S²)] - M² (1-M²ⁿ)/(1-M²)
4. Finally:
   SD²(n) = log{1+SD²(n) / Mean²(n)}
   M(n) = (1/2)log[Mean²(n)/{ 1+SD²(n) / Mean²(n) }]

>Please! Just give the final result!

Assume that the Mean and Standard Deviation of portfolio returns are M and S and the Inflation Rate is i (so I=1+i is the inflation factor). Then probability that the portfolio will survive n years with an initial withdrawal rate of W, increasing with inflation, is N(X) where N is the "standard" normal cumulative distribution function and X = log(1/W) - (1/2)log[Mean2/{ 1+SD2 / Mean2 }] SQRT{log[1+SD2/Mean2]} and log is the natural logarithm, and Mean = M (1 - Mn) / (1 - M) SD2 = (M2+S2) [1-(M2+S2)n] / [1-(M2+S2)] - M2 (1-M2n)/(1-M2) and M = I e-(M - S2/2) S2 = M2[eS2-1] example: M = 0.10 (10% mean return), S = 0.20 (20% volatility), n = 30 years i = 0.03 (3% inflation) so I = 1.03 and W = 0.05 (5% withdrawal rate). Then M = 0.9508, S2 = 0.0369. Mean = 15.073, SD2 = 4.4016. Then X = 2.111 and N(X) = 0.983   or   98.3% probability of survival.

>That's it? Can't you simplify so that ...
That's left as an exercise ... for you!  
But, for reference, there's a picture here.

>That 98.3% you got. Isn't that high, for a 5% withdrawal rate?
Yes. Monte Carlo simulations will give a lower survival rate. However ...

>So your formula is a feel-good formula, eh? It disguises the true ...
Be fair! It's my attempt to generate some formula so as to avoid a jillion Monte Carlo simulations every time you change parameters. Our formula assumes continuous compounding where, if the mean annual return is r, then instead of using (1+r) as the mean annual gain factor, we use e^r. That increases the gain. For example, a 10% mean annual gain would turn into a mean gain factor of e^0.10 = 1.1052 corresponding to a 10.52% annual return.

>So, fix it!
Well, if it were me, I'd want to replace e^r by 1+r which I could do by entering, in place of r, the number log(1+r).
For example, if I wanted to use the above formula with r corresponding to 10%, then I wouldn't use r = 0.10 in the formula.
Instead, I'd use log(1+r) = log(1.10) = 0.0953 meaning a 9.53% return.

Okay, here's what we'll do:

1. Our $1.00 portfolio, after n years, is g₁g₂...g_n[1 - WgMS(n)].
2. g₁g₂...g_n is just the Buy-and-Hold Portfolio (without withdrawals).
3. We look at just the factor [1 - WgMS(n)].
4. This factor gives the fraction of the Buy-and-Hold Portfolio (after n years) with withdrawals.
5. If W is large (or returns are small!), then [1 - WgMS(n)] may be negative in which case our portfolio with withdrawals will be negative. Such a portfolio didn't survive n years!!
6. Suppose that F(x) is the cumulative distribution function for gMS(n).
7. Then F(x) gives the fraction of portfolios for which gMS(n) is less than x.
8. In general, if gMS(n) is less than x, then 1 - WgMS(n) will be greater than 1-Wx.
9. Hence F(x) is the fraction of portfolios whose value is greater than (Buy-and-Hold Portfolio)*(1-Wx).
10. Hence 1-F(x) is the fraction of portfolios whose value is less than (Buy-and-Hold Portfolio)*(1-Wx).

>I haven't the faintest idea what you ...
Okay, here's an example where we refer to the numbers above:

• 4:
  If 1-WgMS(30) = 0.45 then our portfolio with withdrawals is 45% of the Buy-and-Hold Portfolio, after 30 years.
• 7:
  If F(21) = 0.12 then 12% of portfolios will have gMS(30) less than 21.
• 8:
  If gMS(30) is less than 21, then (for a 4% withdrawal rate) 1-WgMS(30) is greater than 1-0.04*21 = 0.16
• 9:
  Since F(21) = 0.12 then 12% of portfolios will be greater than 0.16 of the Buy-and-Hold Portfolio.
• 10:
  Then 1- F(21) = 1-0.12 = .88 or 88% of portfolios will be less than 0.16 of the Buy-and-Hold Portfolio.

In our case, G(x) = 1 - F(x) gives the probability that 1 - WgMS is less than 1-W x.
So, if we plot 1 - F(x) versus u = 1-W x we'd get something like this:

It's saying that, for the given parameters, 33% of our portfolios will be less than 10% of the Buy-and-Hold Portfolio, 62% will be less than 20% and 90% will be less than 30% of the Buy-and-Hold Portfolio.
>And 11.8% of the portfolios will be dead, eh?
Yes, 11.8% are negative, after 30 years of withdrawals starting at 5.0% ... increasing with inflation.
>Do you really believe this stuff?
Should I? However, it's fun to play with, so there's a spreadsheet. Just RIGHT-click and Save Target here.

for Part III