How long till you're broke?
We have $B in our portfolio and it's earning an annual return of R (for a 12.3% return, we put R = .123).
At the end of each year we withdraw $P, increasing with inflation,
which we assume is I (I = .03 means 3% annual inflation).
We start with a portfolio worth B and we'll track the balance at the end of each year:

After 1 year our portfolio has grown to B(1+R), and we withdraw P(1+I).
(See? It's increased ... with inflation!)
Our portfolio is now worth
B(1+R) - P(1+I).

To avoid getting too messy, we'll let
x = (1+R) and y = (1+I)
so, after ONE year (and ONE withdrawal), our portfolio is worth Bx - Py

By the end of the second year this portfolio has increased by a factor x = (1+R) to
Bx2 - Pxy and we withdraw another $P increased by two years of inflation,
which means we withdraw Py2, leaving a portfolio of Bx2 - P xy - y2.

There's a magic formula we can use here. It's
x2 + xy + y2 = (x3 - y3)/(x - y)
In order to take advantage of this magic formula, we rewrite the balance in our portfolio as:
(B + P)x2 - P(x2 + xy + y2)
Using the magic formula, it's:
(B + P)x2 - P(x3 - y3)/(x - y) after TWO years and TWO withdrawals.

We jump ahead to the end of the Nth year. Your portfolio is now:
(B + P)xN - P(xN+1 - yN+1)/(x - y) after N years and N withdrawals
(... and we've used that magic formula again ... and again!)

Alas, that last withdrawal left us with a ZERO portfolio:
(B + P)xN - P(xN+1 - yN+1)/(x - y) = 0.

So what's N, the number of years until our portfolio ran dry?

We suppose (to make life simpler) that we withdraw our first $P at the very start,
so our original Portfolio is reduced from B to B - P and B+P becomes just B.

We also let z = x/y = (1+R) / (1+I),
we can rewrite the above equation like so:
[!]    B = P (1 - z-N)/(z - 1)
If we solve for N (left as an exercise! *) we get:
N = -log(1 - (B/P)(z - 1)) / log(z)
SO, if we know B and P and x = (1+R) and y = (1+I)
we can compute z = (1+R) / (1+I), hence N.

Here's a calculator to play with:
Annual Return on Investment (example 7) =%   Annual Increase in Portfolio
Annual Inflation Rate (example 3) =%   Annual Increase in Withdrawal Amount
Initial Withdrawal Rate (example 7.5)=%   (Initial Withdrawal)/(Initial Portfolio), increasing with Inflation
Years to Zero =

... and that's also what this spreadsheet does. Just RIGHT-CLICK here and Save Target or Save Link to download.

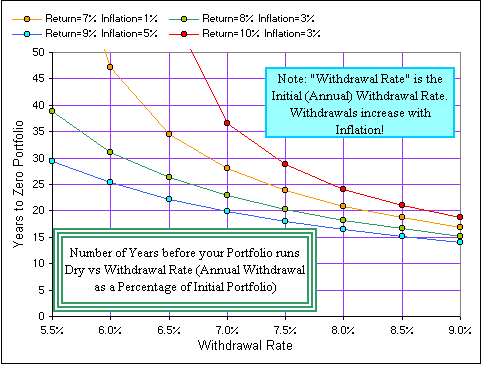
One more thing:

The Ratio B/P = (1 - Z-N) / (Z - 1) gives a Magic Multiplier, namely how large your portfolio should be compared to your desired annual withdrawal (the withdrawals increasing with inflation). If you want your portfolio to last for thirty years, you get the following:

For example, if you assume 4.0% inflation and 7.0% return on your investments - both constant for thirty years after you begin withdrawals (fat chance!) - then the Magic Multiplier is about 20, meaning that if you want $50,000 annually from your portfolio (increasing with inflation) you should have 20 x $50,000 = $1,000,000 in your portfolio.

* The equation [!] can be rewritten in the form:
z-N = 1 - (B/P)(z - 1)
then take the logarithm of each side.

P.S. If you want the formula when the first withdrawal is after one year (instead of immediately), then just replace B by B + P in [!].

P.P.S. If I = 0 (no "inflation" ... we withdraw equal amounts at the end of each year),
then y = (1 + I) = 1 so z = x = (1 + R)
If we let also let N be months (instead of years), and
interpret R as the monthly rate (instead of the annual rate),
then (whooee!) [!] gives the monthly payments, $P, for an N-month mortgage of amount $B:
P = BR / (1 - (1+R)-N)

... ain't Math wunnerful?

Okay, all the above assumes a constant rate of return. Does that really happen, in real life? Hardly. To get some idea of what could happen with REAL investments, where the gain increases, decreases, is larger, then smaller, sometimes positive, sometimes negative ... see Portfolio Growth.