Okay, here's what we're doing: Each day we calculate the Percentage Range (PR) of stock prices as the Maximum of: 100*[ (today's High)- (today's Low) ] / (yesterday's Close) 100*| (today's High) / (yesterday's Close) - 1 | 100*| (today's Low) / (yesterday's Close) - 1| Then we calculate the 20-day Exponential Moving Average (EMA) of these daily PRs to get the APR, according to:       APR(today) = (1 - 1/20) APR(yesterday) + (1/20) PR(today) Then we take 1% of the money we have to invest (our "Equity") and divide by today's (APR)*(Stock Price) to get:       gST = (1% of Equity) / [ (APR)*(Stock Price) ] >And that gives the number of shares we buy? Well, that or a multiple of that. Our trades are 1 gST or 2 gST ... or whatever. However, if'n you buy lots of stocks, you'll need lots of money. Here are some DOW stocks Note that we calculate APR as a percentage, not a decimal. That is, for a 2.5% average/maximum 20-day variation, we take APR = 2.5, not 0.025. >That COST is what it'd cost to buy that many shares? Yes, to buy 1 gST of each, assuming $100K Equity ... so 1% of Equity is $1K. >So what's the TOTAL cost? You don't wanna know. ($458K) >So what does gST stand for? good Stock Trade. >Or gummy Stock Trade? If you say so.

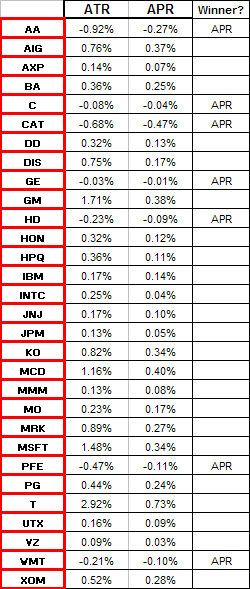
Table 1

• For two assets X and Y with the same price, if the daily volatility of X (measured by APR) is twice that of Y, then you'd buy half as many shares.
• If the price of X were twice that of Y, you'd invest the same dollar amount in each.
• If you were considering investing in a basket of stocks (perhaps a few of the DOW stocks), then gST would provide an allocation of your Equity.
• There is nothing sacred about a 20-day average. A common average for ATR (or APR?) is 14 days.
• There is nothing sacred about 1% of your Equity. The gST will provide guidance concerning the relative amounts of each asset you'd buy.
• Note that APR*(Stock Price) gives some estimation of the maximum daily variation in stock price.
  • If APR = 1.2% and Stock Price = $20, then APR*(Stock Price) = 1.2*20 = 24.
  • That suggests that each share of the stock could vary by as much as $0.24 on a given day.
  • If you had gST shares of the stock, that'd imply a daily variation as large as gST*APR*(Stock Price).
  • If you wanted to ensure that such a daily variation didn't exceed 1% of your Equity, then you'd want to consider having:
        gST*APR*(Stock Price) = (1% of Equity).
  • That'd make:
        gST = (1% of Equity) / [ APR*(Stock Price) ]   ... which, of course, is the way we defined gST
• If you think that this is the way to preserve your financial health, you might also consider tylenol.

>Aha! I thought that was a typo in the heading of this tutorial.
I wouldn't want to blame anybuddy for TURTL. It could be a lousy method and ...

>Haven't you backtested it yet?
Patience. I haven't finished. We have to talk about WHEN to buy (or sell).
However, before I do that, let's look at a spreadsheet that'll compare gST for various stocks, like so:

You type in up to 30 stock symbols and click a button and you get a set of associated gSTs and the COST of buying that many shares at the current stock price.

>Aha! That's where you got Table 1, right?
Right. That's using APR rather than ATR.
Look closely and you can see that you should spend twice as much money on AA as AIG: $10K vs $5K. It's quite a different ratio if you use ATR.
Indeed, their APRs are 10% and 20% so you see that the more volatile stock ...

>And you all believe this stuff?
Of course! Whenever I see a neato mathematical ritual I get all excited and figure "How can it be wrong?"

>Yeah, sure. Is that why your portfolio is down 30% this year?
Shhh ...

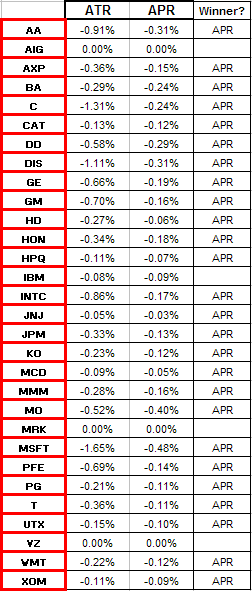
>So how do things compare when you use ATR instead of APR? Aaah, good question! We consider the two prescriptions: For ATR we use the maximum value of: (today's High) - (today's Low) | (today's High) - (yesterday's Close) | | (today's Low) - (yesterday's Close) | For APR we use the maximum value of: 100 [ (today's High)- (today's Low) ] / (yesterday's Close) 100 | (today's High) / (yesterday's Close) - 1 | 100 | (today's Low) / (yesterday's Close) - 1| In other words, for APR, the ratios are relative to (yesterday's Close). That makes them percentages. That makes them independent of the currency. In Japanese yen or British pounds we'd get the same ... >Are you going to answer my question? Huh? Oh, yes ... how they compare. Check out Table 2: >Uh ... so how much of each should we you buy? Can you show the relative amounts so that ...? Okay, suppose we compare each investment with a $100 investment in that first stock: AA. You'd get Table 3: Note that the allocations are quite different and ... >Which is better? ATR or APR? Uh ... give me a chance to backtest. >And you haven't said WHEN to buy and sell! Patience!! Table 3

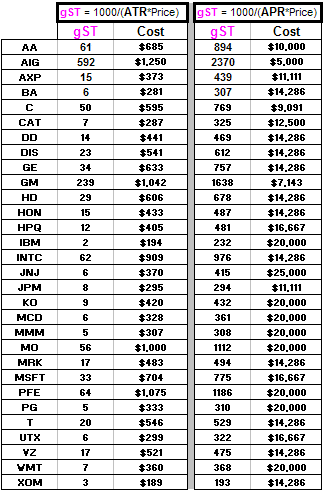Table 2

When to BUY & SELL

Remember when we talked about Donchian Channels? >No. Then read all about them here, because that's what the Turtles used to determine when to Buy or Sell. We look at the highest High and the lowest Low over the past 20 days. That gives the upper and lower parts of the Donchian Channel. When the current stock price moves above the upper Donchain, that's interpreted as the beginning of an uptrend. ... so we BUY a UNIT (or maybe 2 or more UNITs, depending upon the market we're considering). When the current stock price moves below the lower Donchain, that's interpreted as the beginning of an downtrend. ... so we SELL a UNIT . >So what's better? Using ATR or APR? Using an ATR UNIT or an APR gST? Using ...? Patience. I'm still working on it ... Okay, here's what I get: Nov/05 - Nov/06 Nov/07 - Nov/08 Nov/05 - Nov/06 Nov/07 - Nov/08

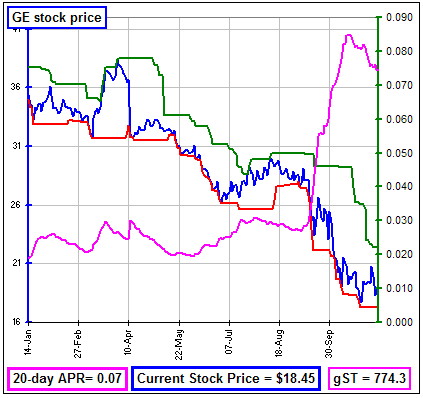>Okay ... so what's better? ATR? APR?
Uh ... can I flip a coin?