Look carefully at Figure 1: You buy a lottery ticket and your personal Utility Function is U(x) ex: U(x) = SQRT(x) The lottery has two possible results: you win either $A or $B ex: A = $2,000, B = $10,000 You attach a Utility value to each possible result: U(A) and U(B) ex: U(A) = SQRT(2000)= 44.72 and U(B) = SQRT(10000) = 100 The probabilities for each are p and q = 1 - p ex: p = 0.75 or 75% then q = 0.25 or 25% Your expected winning is then E[x] = pA + qB ex: E[x]=0.75*2000 + 0.25*10000 = $4,000 The Utility you attach to this Expected value is U(E[x]) ex: U(E[x]) = U(4000) = SQRT(4000) = $63.25 The Expected value of your Utility is E[U(x)] = pU(A)+qU(B) (as opposed to the Utility of the Expected Value!) ex: E[U(x)] = 0.75*44.72 + 0.25*100 = 58.54

Figure 1

>Wow! That's confusing. So many numbers and ...
Think of it this way:

• There are two possible winnings, $2K and $10K, and an Expected winning of $4K, shown as blue dots on the x-axis.
• However, you attach a personal value to each, namely 44.72 and 100 (so, to you, personally, the second isn't worth five times more but just a bit more than twice as much).
• Further, since there is a 75% chance of achieving the 44.72 and a 25% chance of achieving the 100, the Expected value of the Utilities you've assigned is E[U(x)] = 0.75*44.72 + 0.25*100 = 58.54.
• So, what's important to you are the red dots on the y-axis (not the blue dots on the x-axis).

>But there's another red dot on the x-axis called V. What's ...?
That's where it gets interesting.
Suppose that there are two lotteries. The one we described above and one which pays a guaranteed E[x]. There aren't two probabilities associated with this second lottery; every time you play, it pays E[x], guaranteed. The Utility associated with this second lottery is no longer a probabilistic combination of two utilities. It's just U(E[x]), the Utility of the Expected value, shown as the green dot on the y-axis.

Have I mentioned that Figure 1 isn't to scale. I mean ...
>I noticed that. Please continue.
Okay. We associate U(E[x]) with the risk-free lottery and we associate E[U(x)] with the risky lottery (where there are probabilities associated with the possible winnings). Because we're risk-averse, we've attach a smaller utility to the risky lottery (namely 58.54 instead of 63.25, in our example, above), even though the Expected income from each lottery is the same, namely pA + qB.

>The risky lottery has a Utility on that straight line and the risk-free lottery is above it, on the Utility curve, right?
Yes, very good. Okay, now we consider a third lottery which pays ...
>What! A third ...?
Pay attention. This third lottery is also a risk-free lottery; it guarantees a winning of $V ... that other red dot, on the x-axis. Because, as you correctly noted, a risk-free lottery has its Utility on the Utility curve, then it has the same Utility as the Expected Utility for the risky lottery.

>Mamma mia!
So what does that mean?

>I have no idea. My head is spinning and ... Consider these two lotteries: the first and the third. One is risky and one is risk-free, but they both have the same Expected Utility. Which would you prefer to play? >If I'm only interested in the Expected Utility ... and it's my Utility, after all ... then why would I choose one over the other? They have the same utility. Exactly! You'd be indifferent to the lotteries. In your mind (meaning in your Utility-conditioned-point-of-view), they're equivalent. Yet the risk-free lottery only pays $V which is less than the Expected winnings for the risky lottery which is E[x] = pA+qB. The utility of this third certainty-equivalent lottery is the same as that of the random lottery. This third, risk-free lottery (which you'd be comfortable in choosing as a replacement for the risky lottery) pays the certainty equivalence to pA + qB, namely $V. >I'd be comfortable? You kidding?

Figure 2

Well, what I mean is, you'd be indifferent between receiving E[x] (with the associated risks) or the lesser amount, $V, with certainty.

>I'm not sure. Maybe, if I liked risk ... I mean, I could win $10K, right?
Yes, but if you're NOT indifferent to $V and E[x] then you've chosen a lousy Utility Function, one which doesn't reflect your personal risk profile.

>I chose it? You kidding? It was your idea ... besides, you haven't mentioned the value of $V. Okay, here's a picture ... to scale The value of $V is $3427. The difference between the Expected value of the risky lottery (namely E[x] = $4000) and the certainty-equivalence (namely $V = $3427) is called the Risk Premium: $4000 - $3427 = $573. >It's how much you'd be willing to forego by choosing a risk-free lottery, right? Yes ... according to your personal Utility Function. >It's how much more you hope to make by taking on the risk, right? Yes. You'd be willing to accept a lower payoff, namely $V, if it's guaranteed ... or, the higher payoff for the random lottery. It doesn't matter to you. They have the same Utility.

Figure 3

>So, isn't there a formula?
Yes, for a U(x) = SQRT(x) Utility Function, it's: Risk Premium: π = pA + qB - {p SQRT(A) + q SQRT(B)}²

and, for the general Utility Function U(x), it's: Risk Premium : π = pA + qB - U^-1(p U(A) + q U(B))
where π is the symbol for the Risk Premium and U^-1(x) is the Inverse of the function U(x) ...

>Inverse?
Yes. If y = U(x), then, solving for x you get x = U^-1(y), the Inverse Function.
      If U(x) = SQRT(x) then U^-1(x) = x²     since y = SQRT(x) means x = y²
      If U(x) = x^1/3 then U^-1(x) = x³     since y = x^1/3 means x = y³
      If U(x) = log(x) then U^-1(x) = e^x     since y = log(x) means x = e^y
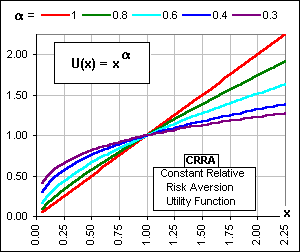
      If U(x) = x^α then ...

>Okay. Fine. I get it. So is all this gonna make me a lot of money in the market? A lot of money? I doubt it. >Then I'd go for the risky lottery. I could make $10K, eh? Right. >So, is there a picture for me? For somebuddy who likes the risk? Who's willing to take the risk     for, maybe, a higher payoff? For somebuddy who'd accept a lower expected payoff for the random lottery because there's a chance that I'd make a bundle. For somebuddy ... Sure. Just flip Figure 2 and we get Figure 4 ... just for you and your risk-loving friends

Figure 4

>Uh ... I should mention that I'd only be risk-loving if I were rich. Then I'd like to take risks. I could afford to lose. I'd enjoy the adrenaline rush with the random lottery ... and the chance for big winnings.
So, if you weren't so rich, then you'd be risk-averse?

>Sure. I'd probably take the guaranteed payoff, even if it paid less. That'd make for an interesting Utility Function, eh? One that changed from concave down to concave up, as I got richer and richer.
Yes, interesting, but richer and richer? You're a dreamer.

>So, what if we both had our own Utility Function. How'd I know if mine was more risk-averse than yours?
We could compare the two Risk Premiums; your π and my π. It turns out that, if - U''(x)/U'(x) is greater for my Utility Function, then my Risk Premium is greater than yours. This is the usual way to compare Utility Functions.

>There we go! Calculus again!
Sorry, but notice that we're comparing the Risk Premiums for each. In fact, R = -U''(x)/U'(x) is called the Arrow-Pratt Measure of Absolute Risk-Aversion, named after ...

>Arrow and Pratt?
Very good. But you mentioned, above, that as your wealth increased, your Utility Function may change from concave down to concave up. In order to include this possibility, we could weight this measure of risk aversion - that's R - by a wealth factor, $x. That'd give x R = - x U'(x) / U'(x), called the ...

>Arrow-Pratt Measure of Relative Risk-Aversion? Very good! And do you remember when we talked about CRRA?       >CRRA? Is that Constant Relative Risk Aversion? Yes. >We talked about it in Part III? Actually, it was in Part II. >No. I don't remember. Why am I not surprised?